Logaritamska funkcija

Logaritam po bazi $a$ broja $y$ je eksponent kojim trebamo potencirati bazu $a$ da bi dobili $y$. Oznaka je $\log _{a} y$.

Gornju vezu između eksponencijalne funkcije i logaritma možemo pamtiti po pravilu "lijevi, desni, srednji". U eksponencijalnoj funkciji, lijevo je $a$, u sredini je $x$, a desno $y$. Kada prelazimo u logaritam, samo ćemo ih posložiti drugim redoslijedom. Primjenimo "lijevi, desni, srednji". Pišemo logaritam, baza je "lijevi" broj, tj. $a$, zatim ide "desni", to je $y$ i na kraju sve mora biti jednako "srednjem", a to je $x$. Isti metodu možemo primjeniti i u drugu stranu, kada želimo iz logaritma preći u eksponencijalnu funkciju.

OPREZ! Jedino na što trebamo paziti kada koristimo ovaj trik je da nam lijevo od znaka jednako uvijek stoji potencija, odnosno logaritam. Ako to zadovoljimo, ostalo je lagano!

Logaritamska funkcija po bazi $a$ je funkcija $f(x)=\log_{a}=x$, gdje su $x$-evi pozitivni realni brojevi i $a>0$.

Graf logaritamske funkcije

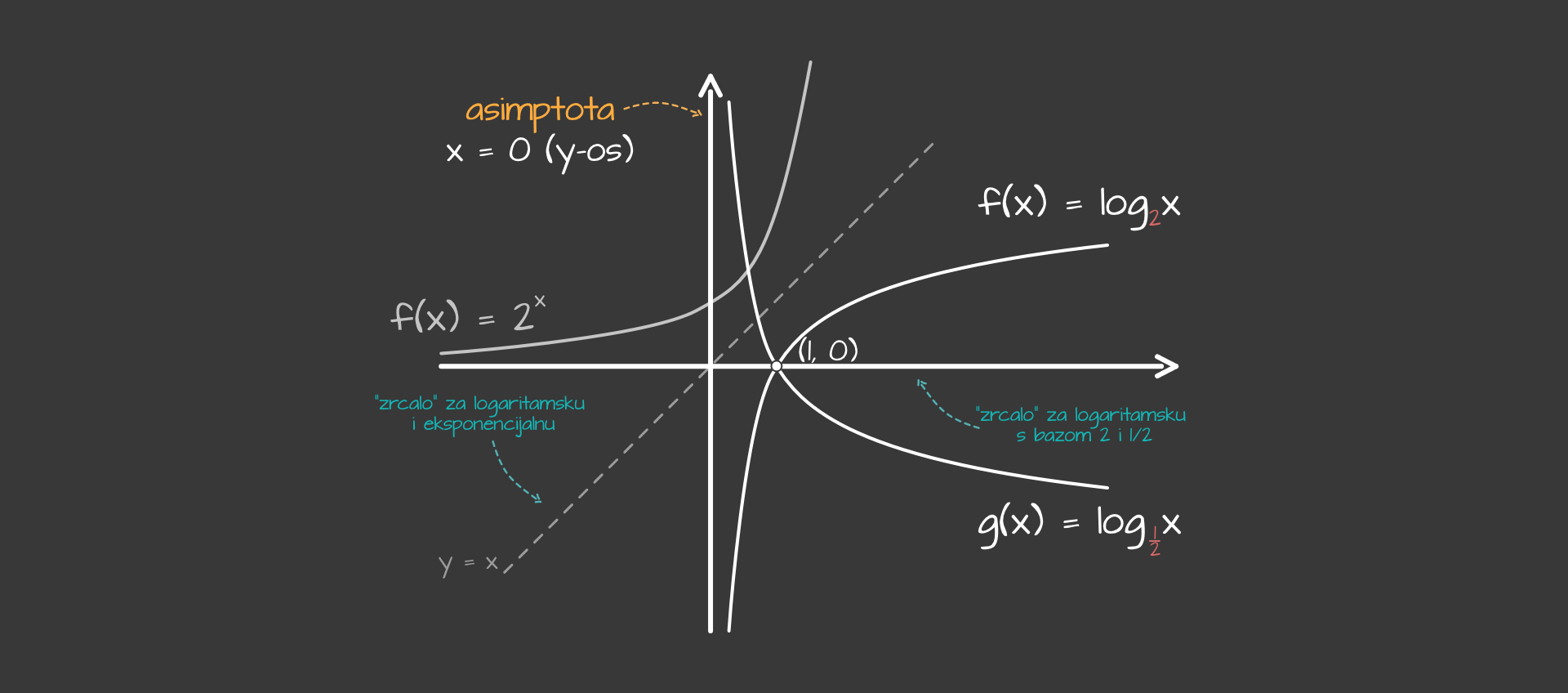
Logaritamska funkcija je inverzna funkcija eksponencijalnoj. Na to možemo gledati kao da je "obrnuta", kao što su recimo kvadriranje i korjenovanje. U koordinatnom sustavu to znači da su im grafovi simetrični obzirom na pravac $y=x$.

• Graf svake logaritamske funkcije oblika $f(x) = \log_{a}x$ siječe x-os u točki $(1,0)$.
• Pomak funkcije po y-osi, tj. gore-dolje, događa se kada funkciji dodamo ili oduzmemo neki broj. Tako će graf funkcije $f(x) = \log_{a}x+b$ izgledati isto kao i obični graf, samo pomaknut za $b$ prema gore ako je $b$ pozitivan ili dolje ako je $b$ negativan.
• Pomak funkcije po x-osi, tj. lijevo-desno, događa se kada $x$-u dodamo ili oduzmemo neki broj. Tako će graf funkcije $f(x) = \log_{a}(x+b)$ izgledati isto kao i obični graf, samo pomaknut za $b$ prema lijevo ako je $b$ pozitivan ili desno ako je $b$ negativan.
• Ako je $a>1$, funkcija raste (kada gledamo s lijeva na desno).
• Ako je $0< a<1$, funkcija pada (opet, kada gledamo s lijeva na desno).
• Grafovi logaritamskih funkcija gdje su baze $a$ i $\frac{1}{a}$, simetrični su obzirom na x-os.
• Grafovi logaritamskih funkcija s argumentima $x$ i $-x$, simetrični su obzirom na y-os.
• Asimptota (pravac kojem se funkcija približava, ali ga nikad ne siječe) logaritamske funkcije $f(x) = \log_{a}x$ je y-os, odnosno pravac $x=0$
• Za $x$ možemo uzeti samo pozitivne realne brojeve, odnosno kažemo da je funkcija definirana za sve pozitivne realne brojeve $x$.
• Funkcija može postići sve brojeve, odnosno kažemo da su svi realni brojevi slika funkcije.

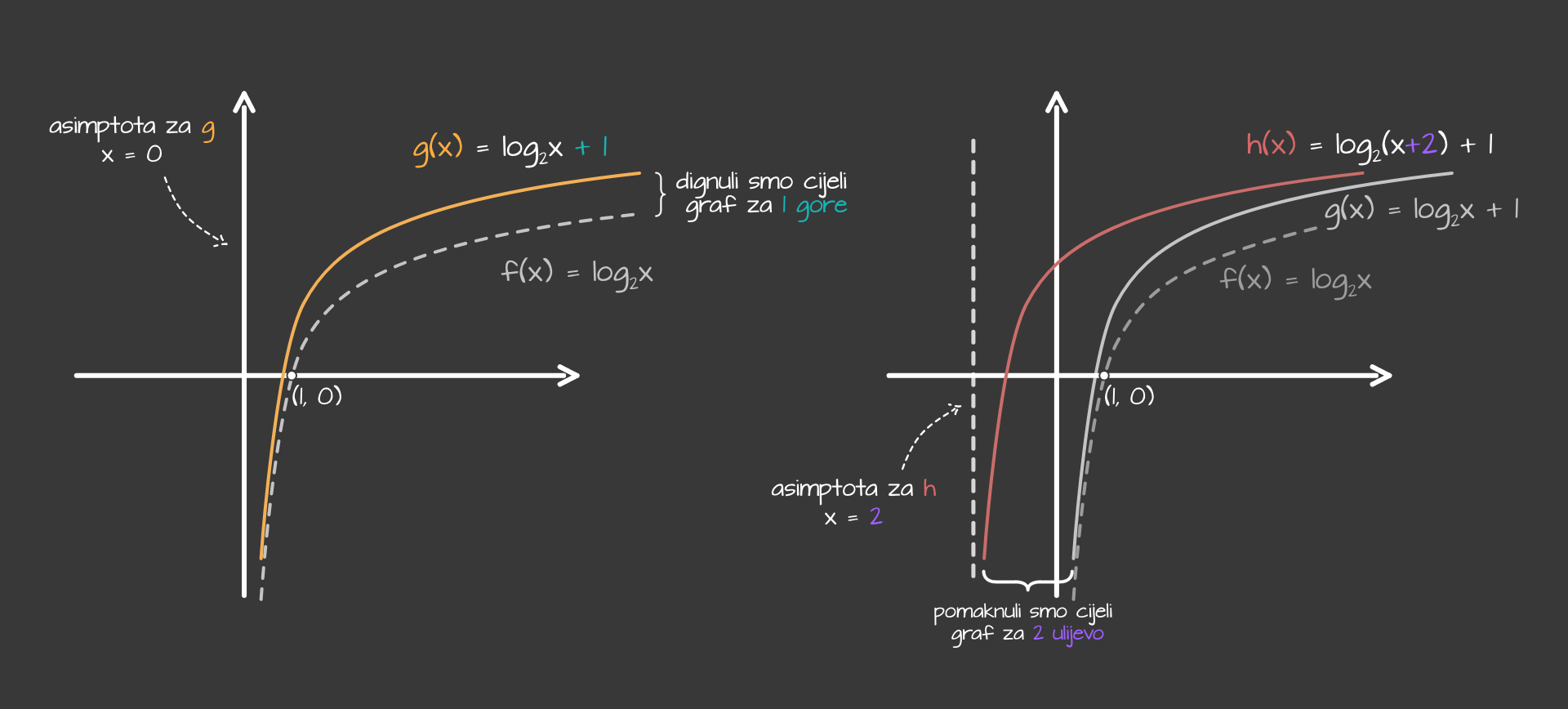
Važni logaritmi

Dekadski logaritam je logaritam s bazom $10$. Oznaka za logaritam po bazi $10$ od $x$ je jednostavno $\log x$.

Prirodni logaritam je logaritam s bazom $e$, gdje je $e$ konstanta koja iznosi $2.71828...$. Oznaka za logaritam po bazi $e$ od $x$ je $\ln$.