2 + 1 GRATIS na pripreme za maturu do kraja rujna!

11d 9h 44m 27s

Mnogokuti

Matematika AMatematika B1. razred
Besplatne materijale donosi ti Cedevita Logo

Mnogokut je bilo koji geometrijski lik s 3 ili više vrhova, odnosno stranica.

Mnogokut se sastoji od jednakog broja vrhova, stranica i kutova.

Dijagonala mnogokuta je dužina koja spaja dva nesusjedna vrha mnogokuta. Imamo formulu za broj dijagonala iz jednog vrha i formulu za ukupni broj dijagonala u mnogokutu.

Broj dijagonala iz jednog vrha u mnogokutu s $n$ vrhova, oznaka je $d_n$.

$ d_n = n - 3 $
Broj dijagonala iz jednog vrha

Ukupan broj dijagonala u mnogokutu s $n$ vrhova, oznaka je $D_n$.

$ D_n = \frac{n \cdot (n - 3)}{2} $
Ukupni broj dijagonala u mnogokutu

Zbroj veličina unutarnjih kutova mnogokuta, oznaka je $K_n$. Zbroj veličina vanjskih kutova mnogokuta iznosi $360^{\circ}$.

$ K_n = (n-2) \cdot 180^{\circ} $
Zbroj veličina unutarnjih kuteva mnogokuta

Pravilni mnogokuti

Pravilni mnogokut je mnogokut kojemu su sve stranice jednake duljine i svi kutovi jednake veličine.

Veličina unutarnjeg kuta $\alpha$ pravilnog mnogokuta računa se formulom:

$ \alpha=\frac{(n-2) \cdot 180^{\circ}}{n} $
Unutarnji kut mnogokuta

Pravilnim mnogokutima možemo opisati i upisati kružnicu. Opisana kružnica prolazi kroz sve vrhove mnogokuta, a upisana dodiruje "iznutra" sve stranice mnogokuta.

Mnogokuti_-_mobile3f5ac4f7bc5139ffd8c0cd404e75e5d0a39b7146

Karakteristični trokut

Karakteristični trokut pravilnog mnogokuta dobijemo tako da središte tog mnogokuta spojimo s dva susjedna vrha mnogokuta. Taj trokut je uvijek jednakokračan. Radijus (polumjer) opisane kružnice čini krakove, a stranica mnogokuta je ujedno i osnovica karakterističnog trokuta.

Mnogokuti_-_mobile_10f370cebb2eec20a49faf6bdb2bdd212450ce9f8

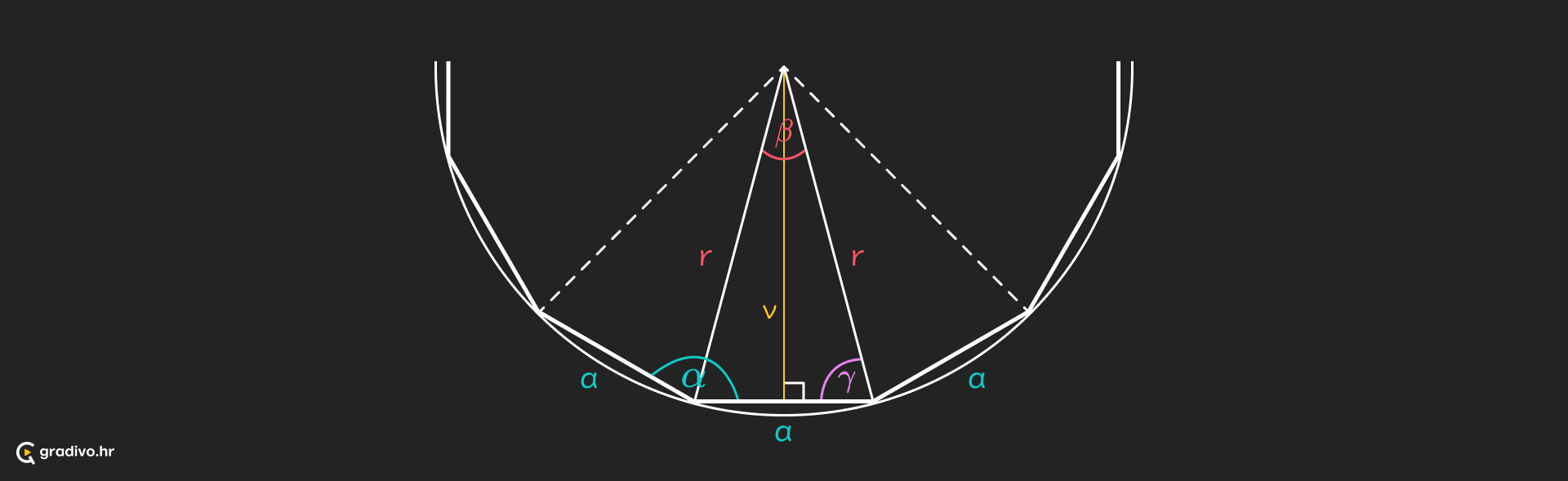
Kutovi karakterističnog trokuta

$ \alpha_{n}=180^{\circ}-\beta_{\mathrm{n}} =\frac{(n-2) \cdot 180^{\circ}}{n} $
Kut pravilnog mnogokuta
$ \beta_{n}=\frac{360^{\circ}}{n} $
Središnji kut
$ \gamma_{n}=\frac{\alpha_{n}}{2} $
Kut uz osnovicu

Trigonometrija karakterističnog trokuta i Pitagorin poučak

$ \sin \gamma_{n} = \cos \frac{\beta_{n}}{2} = \frac{v}{r} $
Trigonometrija karakterističnog trokuta
$ \cos \gamma_{n} = \sin \frac{\beta_{n}}{2} = \frac{a/2}{r} $
Trigonometrija karakterističnog trokuta
$ (\frac{a}{2})^2 + v^2 = r^2 $
Pitagorin poučak u karakterističnom trokutu

Opseg i površina pravilnog mnogokuta

$ O=n \cdot a $
Opseg pravilnog mnogokuta
$ P=n \cdot \frac{a \cdot v}{2} $
Površina pravilnog mnogokuta
Cedevita Logo
ŠTO ČEKAŠ?

Isprobaj potpuno besplatno!

Registracijom dobivaš besplatan*
pristup dijelu lekcija za svaki predmet.

*Besplatan pristup ne zahtijeva unos kartice.
ZA MATURANTEOnline pripremeOD 1. DO 4. RAZREDAOnline instrukcije