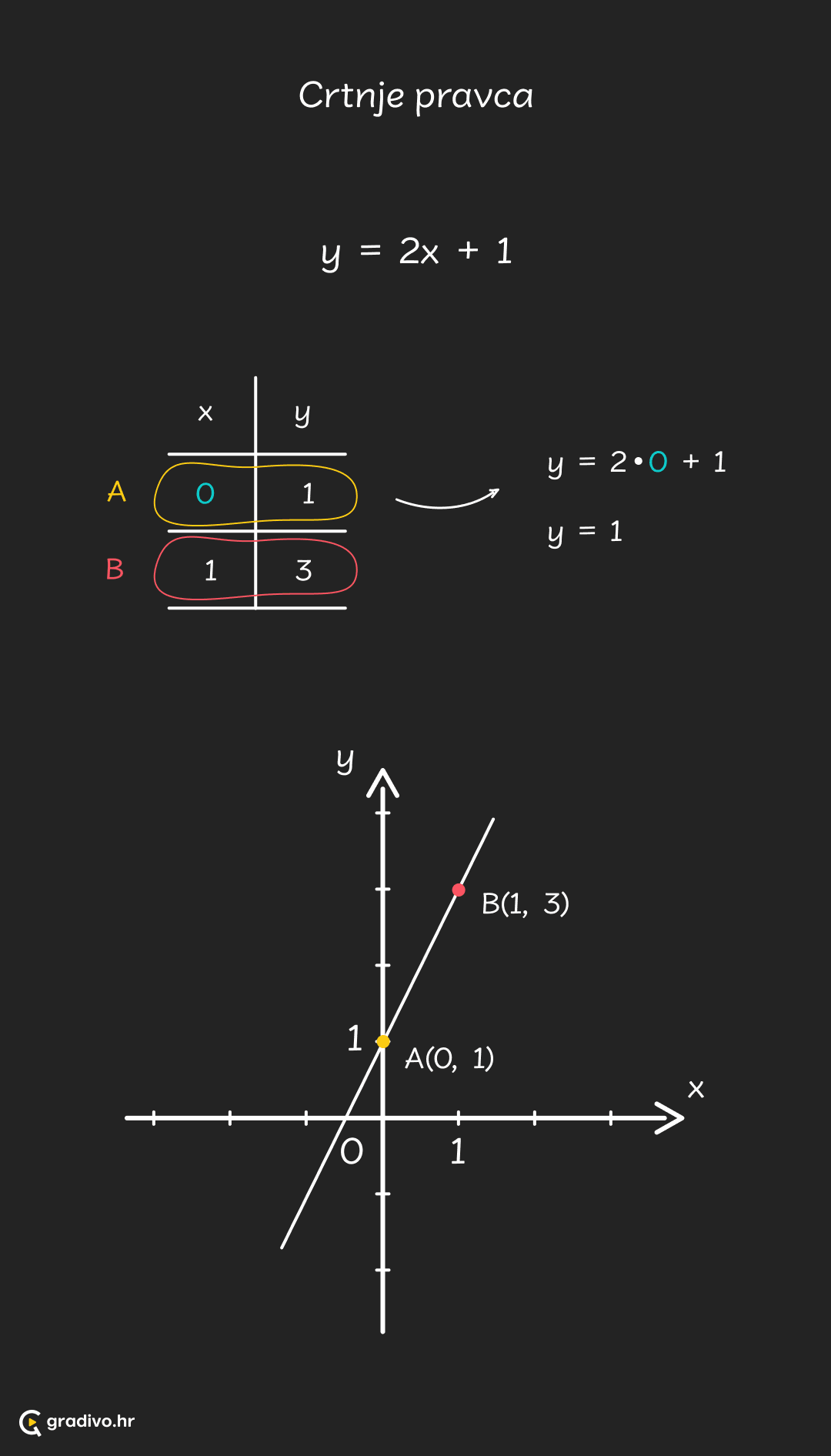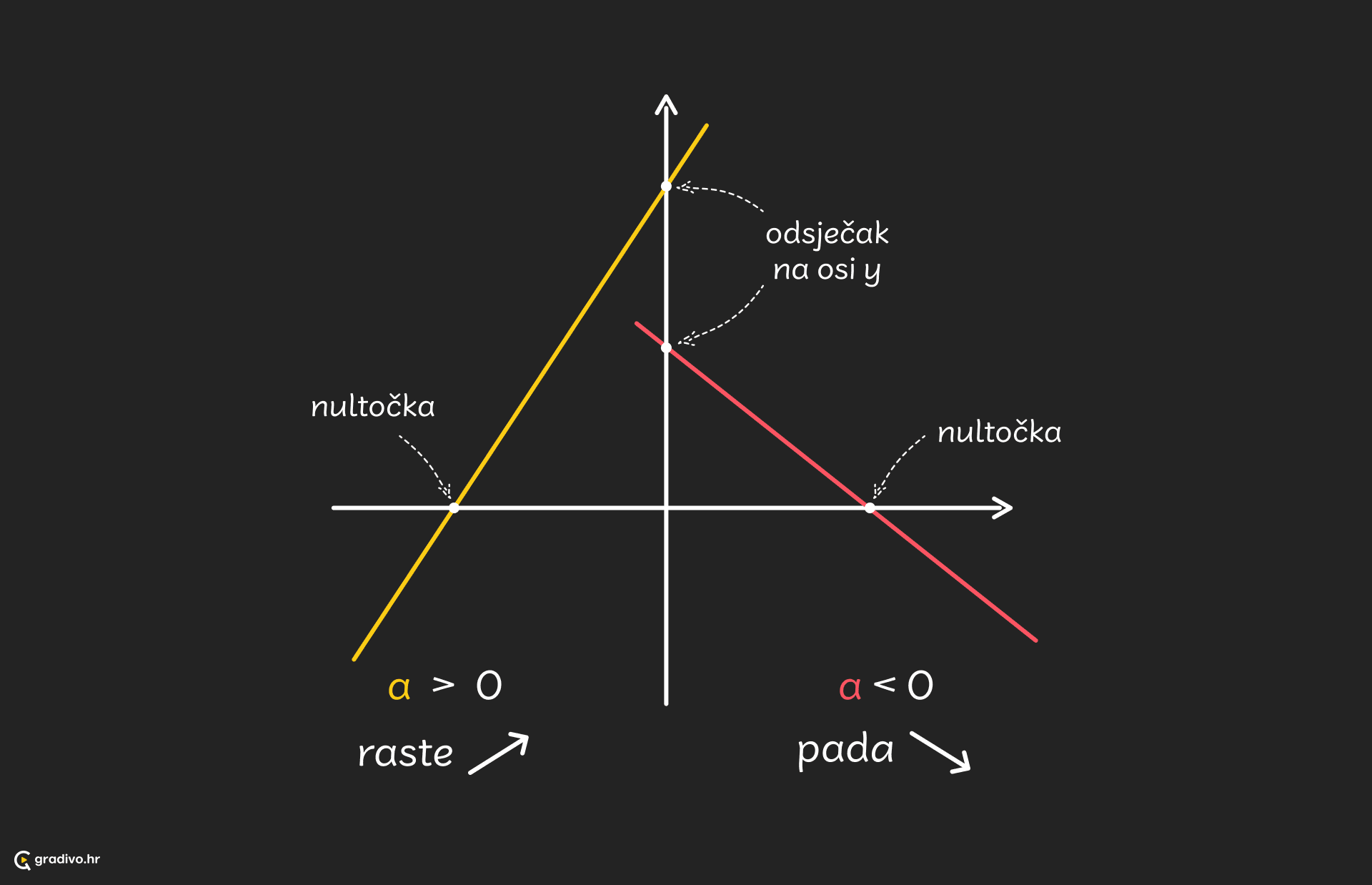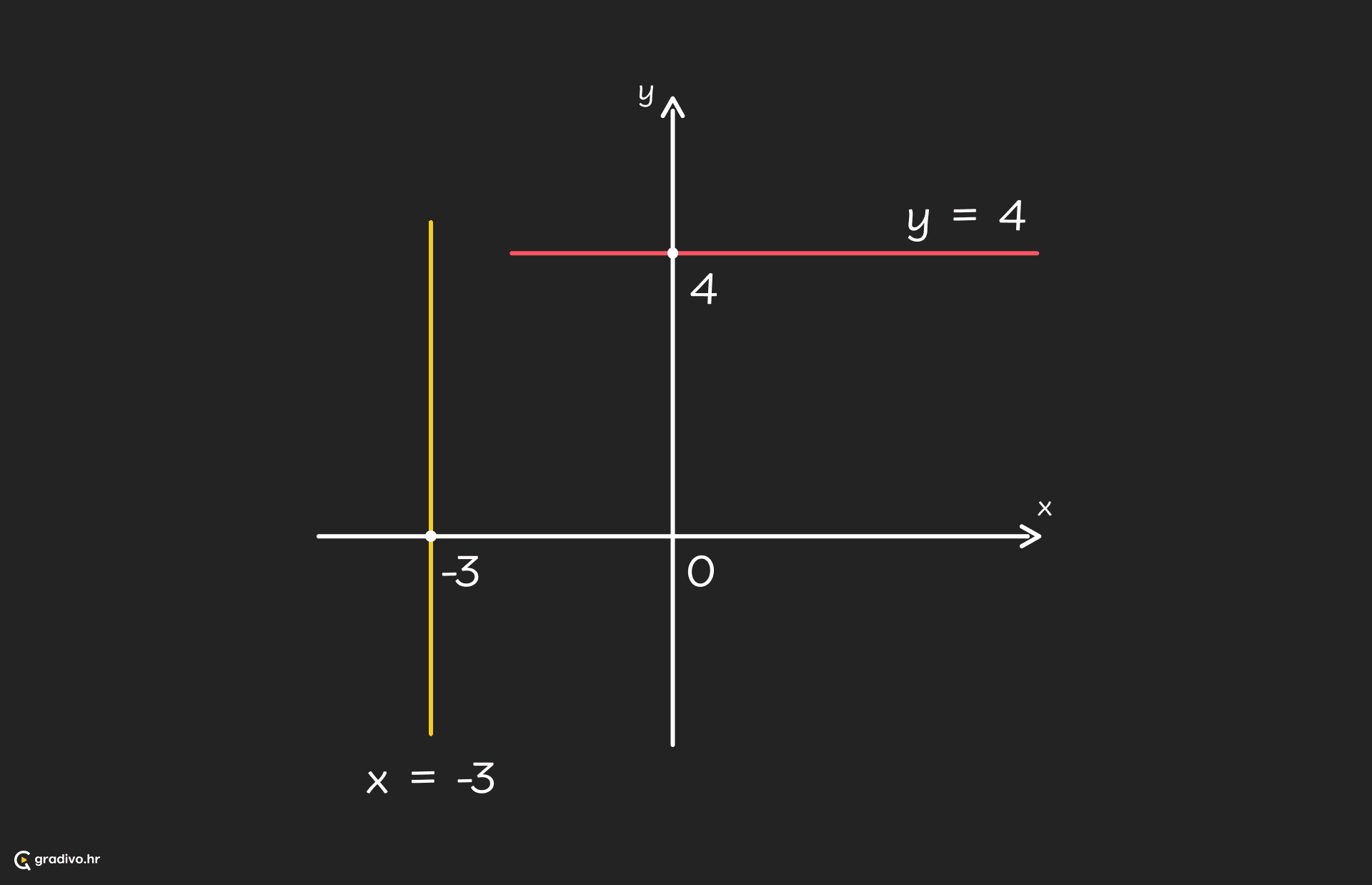Općenito o funkciji
Općenito, funkcija je preslikavanje sa skupa $D$ u skup $K$ takvo da se svaki element skupa $D$ preslika u neki element skupa $K$. Ako se jedan element iz $D$ preslikava u 2 ili više elemenata skupa $K$, onda to nije funkcija. Skup $D$ zovemo domena funkcije, a skup $K$ kodomena funkcije. Provjeru je li neki graf funkcija ili nije, radimo uz pomoć vertikalnog testa. Ako uspijemo naći uspravni pravac koji siječe graf u 2 ili više točke, onda to nije funkcija. Ako svaki takav pravac siječe graf uvijek u samo jednoj točki, onda je to graf funkcije.


Funkciju također možemo zamišljati kao "crnu kutiju" koja radi po nekakvom pravilu. Nakon što u nju ubacimo broj, ona po zadanom pravilu nešto napravi s tim brojem i rezultat izbaci van.
Ako sa $f$ označimo našu funkciju, tada pridruživanje broja $x$ broju $y$ označavamo s $f(x)=y$. Broj $x$ zovemo argument funckije, a $y$ vrijednost funkcije.
Svaka funkcija je zadana svojom domenom, kodomenom i pravilom pridruživanja.
Slika funkcije je skup svih vrijednosti koje funkcija može poprimiti, odnosno skup svih brojeva koje funkcija može izbaciti. To ćemo gledati kao sve $y$-e koje možemo dobiti. Oznaka za sliku je Im.


Funkcija je injekcija ako se svaki $x$ preslika u svoj, drugačiji $y$ tj. ako ne postoje dva $x$-a za koja će funkcija izbaciti istu vrijednost. Injektivnost se provjerava horizontalnim testom. Slično kao i vertikalni test, ako vodoravni pravac siječe funkciju u dvije ili više točkaka, nije injekcija, a u suprotnom jest.


Linearna funkcija
Funkciju zadanu pravilom $f(x) = a \cdot x + b$ gdje su $a$ i $b$ neki realni brojevi i $a \mathrel{\char`≠} 0$ nazivamo linearnom funkcijom. Broj $a$ se zove koeficijent smjera (nagib pravca), a $b$ je odsječak na osi y.
U linearnoj funkciji, umjesto $a$ i $b$ bi trebali stajati brojevi, a $x$ i $f(x)$ (odnosno $y$) ostaju slova.
Broj $a$, nagib pravca ili koeficijent smjera, određuje koliko je pravac nagnut - strm ili blag. Što je $a$ veći po svojoj vrijednosti, to je pravac strmiji.
Broj $b$, odsječak na osi y, predstavlja mjesto gdje pravac udara y-os. To je dakle broj na kojem vidimo da pravac siječe y-os.
Nultočka linearne funkcije je broj $x$ koji dobijemo rješavanjem jednadžbe $ax + b = 0$.
Graf svake linearne funkcije je pravac. Za pravac ćemo reći da raste, ako gledajući s lijeva na desno, idemo sve više i više. U tom slučaju je $a>0$. Obrnuto, ako s lijeva na desno pravac izgleda kao da se spušta, reći ćemo da pada i tada je $a<0$.
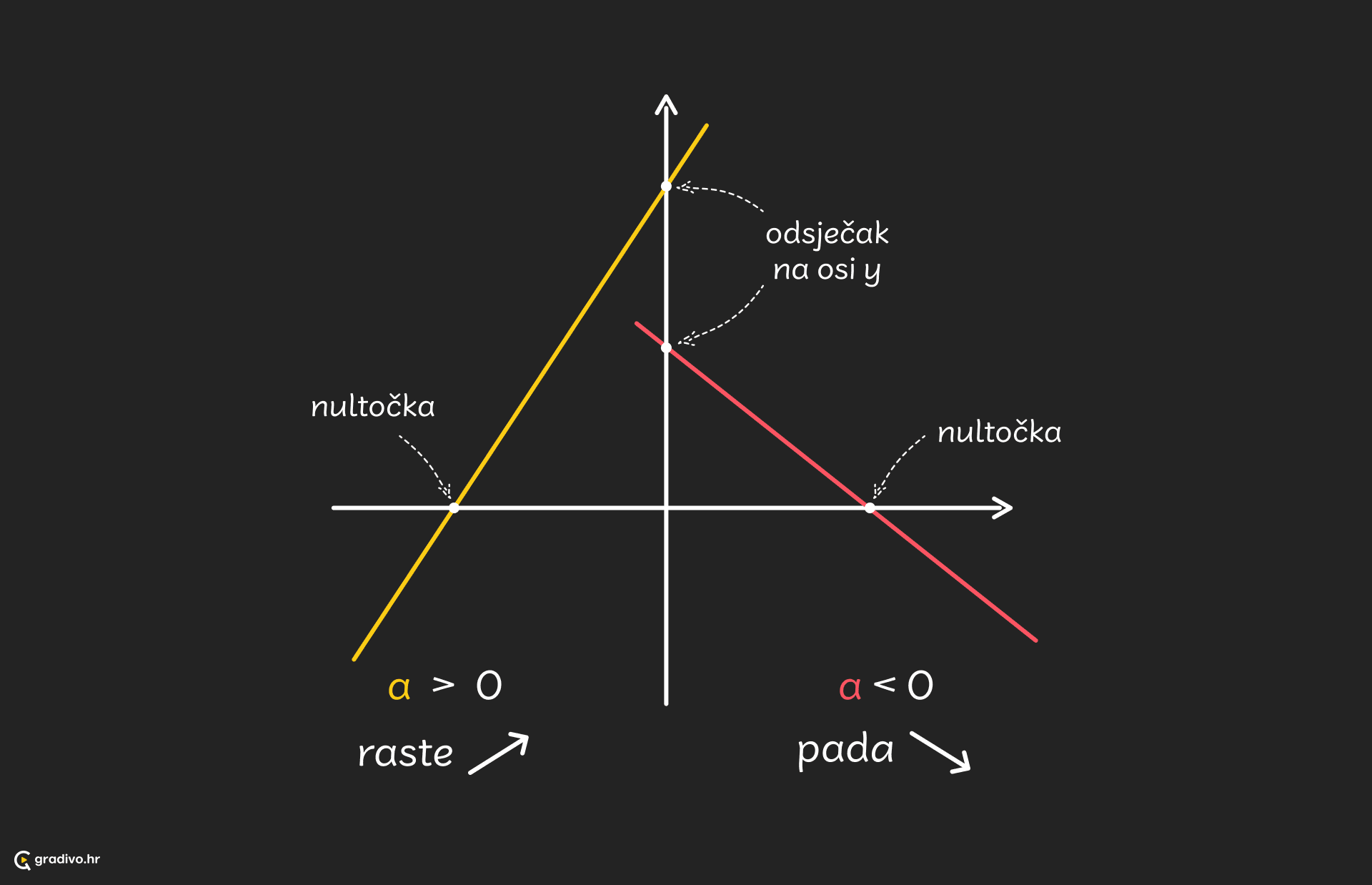

Nagib pravca
Nagib pravca, odnosno koeficijent smjera, nam je jako bitan. Govori nam koliko brzo neki pravac ide prema gore ili prema dolje. Ako ga želimo iščitati iz slike pravca, to možemo vrlo jednostavno napraviti. Trebaju nam samo dvije "lijepe" točke.
Krećemo od lijeve od te dvije točke i gledamo koliko moramo ići dolje ili gore da dođemo do razine druge točke. Naravno, ako se pomičemo dolje, stavljamo minus ispred broja, a ako idemo gore, ne stavljamo ništa. Taj broj će ići gore u razlomak odnosno u brojnik. Nazivnik tj. donji broj u razlomku će biti pomak od lijeve točke do desne, odnosno koliko nam koraka treba u desno da dođemo do njezine razine. Dakle, $a$ će biti jednak razlomku koji nastane iz ova dva broja.


Crtanje grafa linearne funkcije
Znamo da je graf linearne funkcije pravac. Svaki pravac je određen s dvije točke pa nam je zapravo dovoljno naći samo dvije točke koje zadovoljavaju početnu funkciju i odmah možemo nacrtati pravac.
Točke nalazimo tako da za $x$ odaberemo neki broj i za njega izračunamo koliki će biti $y$. Te dvije vrijednosti skupa određuju jednu točku. Postupak ponovimo još jednom i imamo dvije točke kroz koje povučemo pravac.
Ovaj postupak možemo lijepo napraviti preko tablice kako je pokazano na slici dolje.

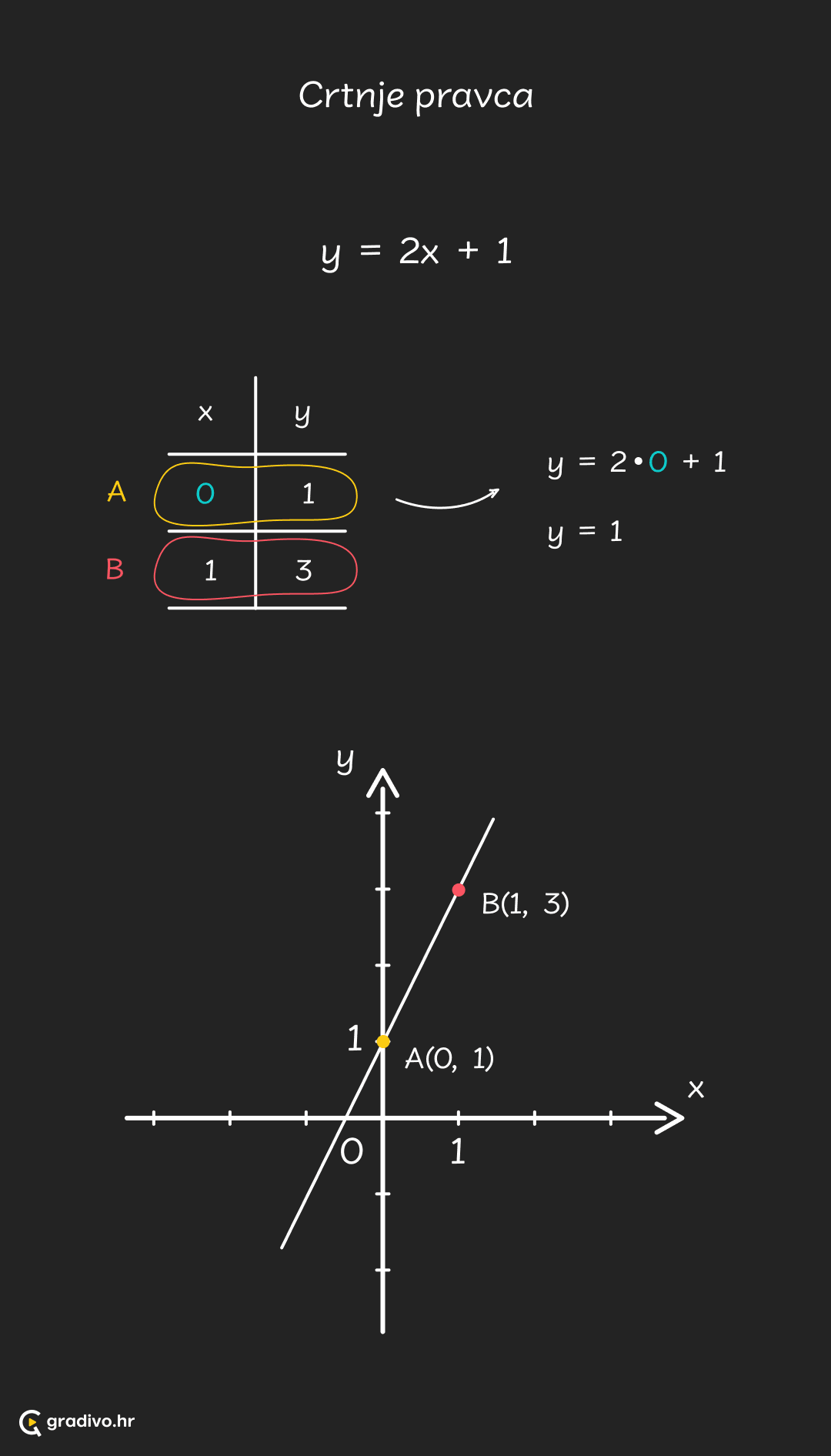
Posebni pravci su takozvani horizontalni i vertikalni pravci.
Horizontalni pravac je oblika $y = b$, gdje je $b$ neki broj. On je paralelan s $x$-osi, tj. osi apscisa.
Vertikalni pravac je oblika $x = c$, gdje je $c$ neki broj. On je paralelan s $y$-osi, tj. osi ordinata.
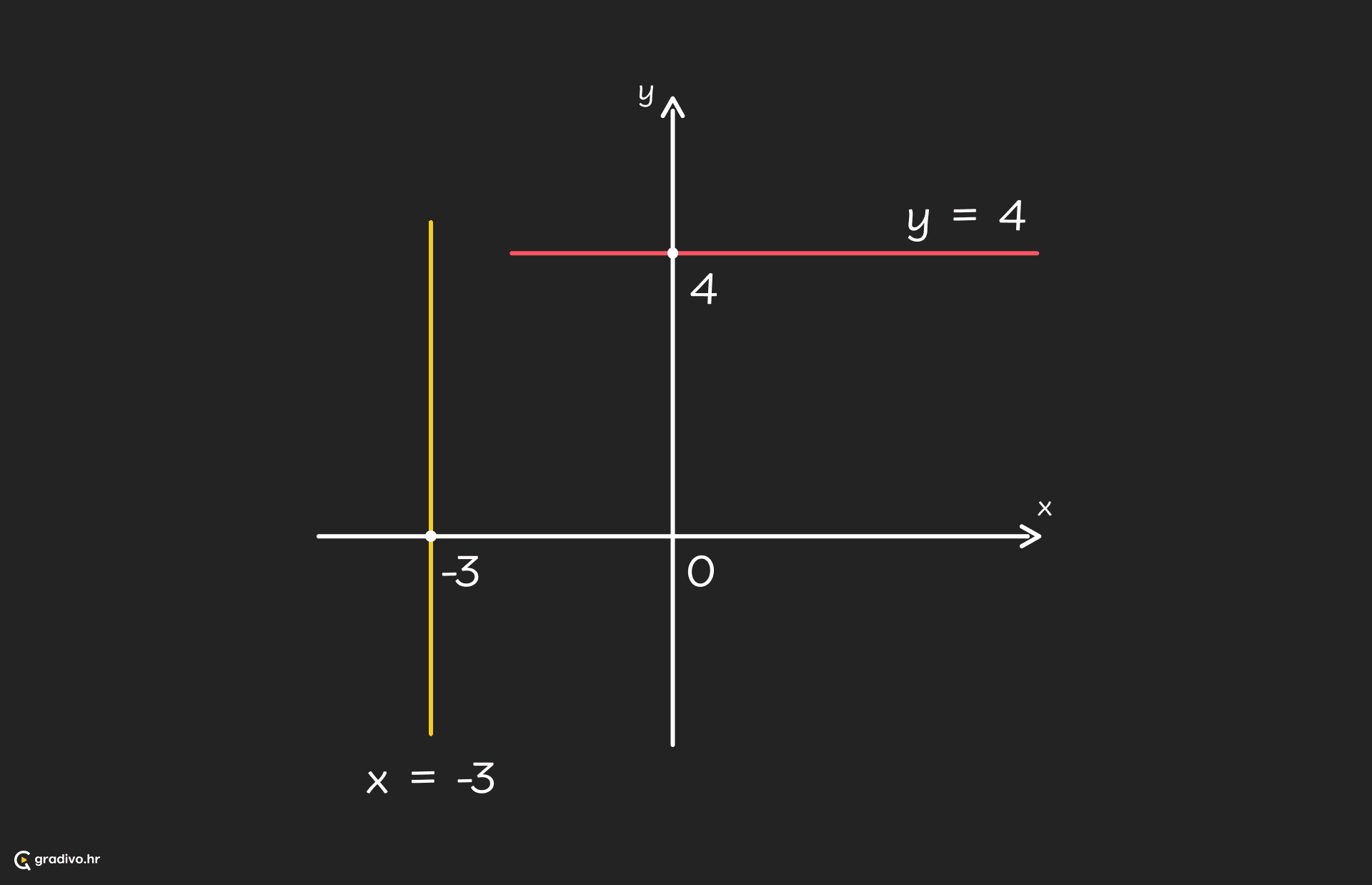

Graf funkcije apsolutne vrijednosti
Graf apsolutne vrijednosti $y=|x|$ crtamo tako da:
1. nacrtamo graf funkcije $y=x$
2. dio funkcije koji se nalazi iznad $x$-osi ostaje nepromijenjen, a dio funkcije ispod $x$-osi prebacimo iznad $x$-osi tj. zrcalimo s obzirom na $x$-os jer funkcija apsolutne vrijednosti svaku negativnu vrijednost pretvara u pozitivnu istog apsolutnog iznosa.
Na taj način ćemo dobiti graf funkcije $y=|x|$.
Graf funkcije $y=|x|$ jednak je grafu $y=x$ za $x\geq0$ i grafu $y=-x$ za $x<0$.