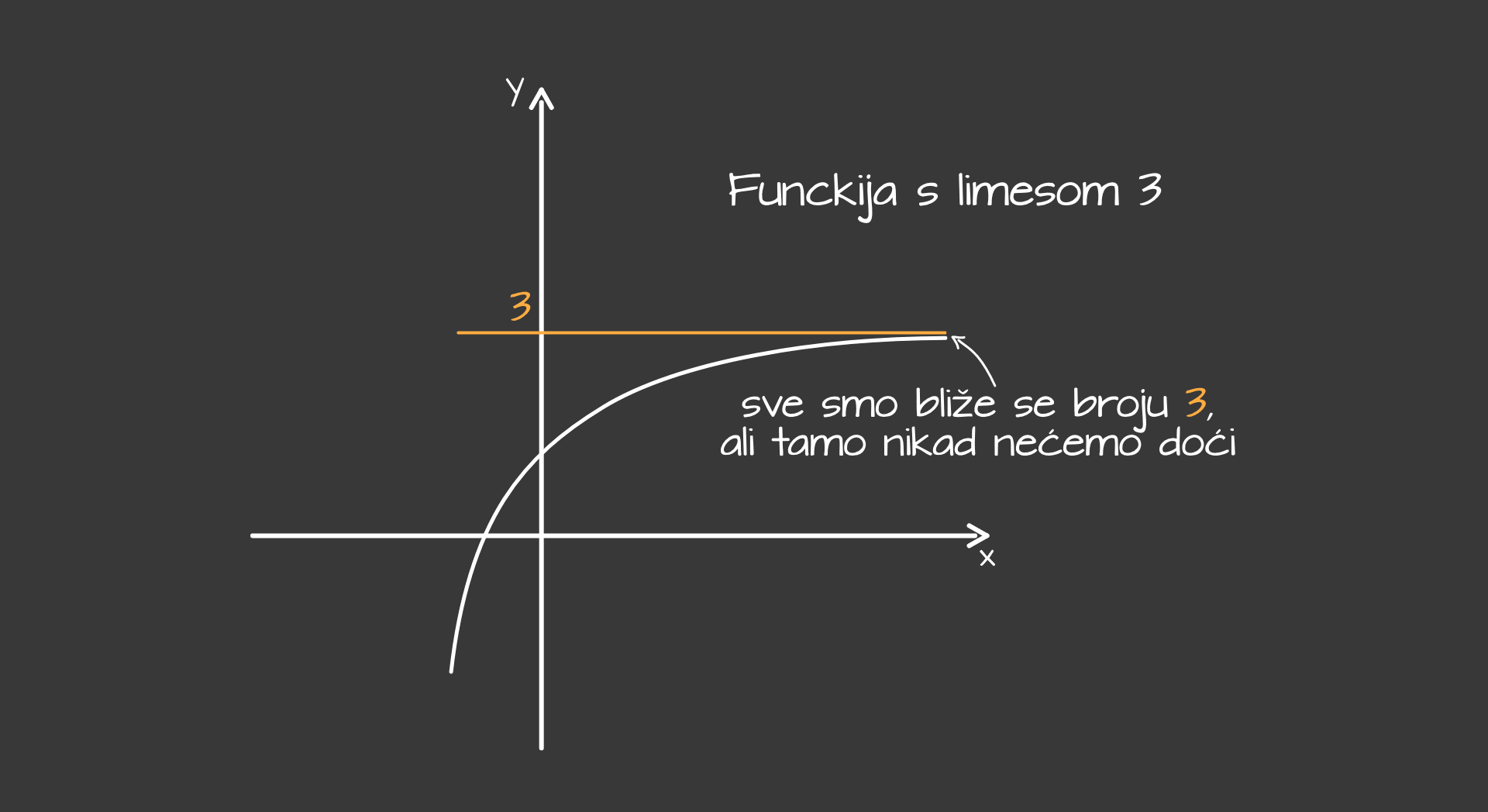
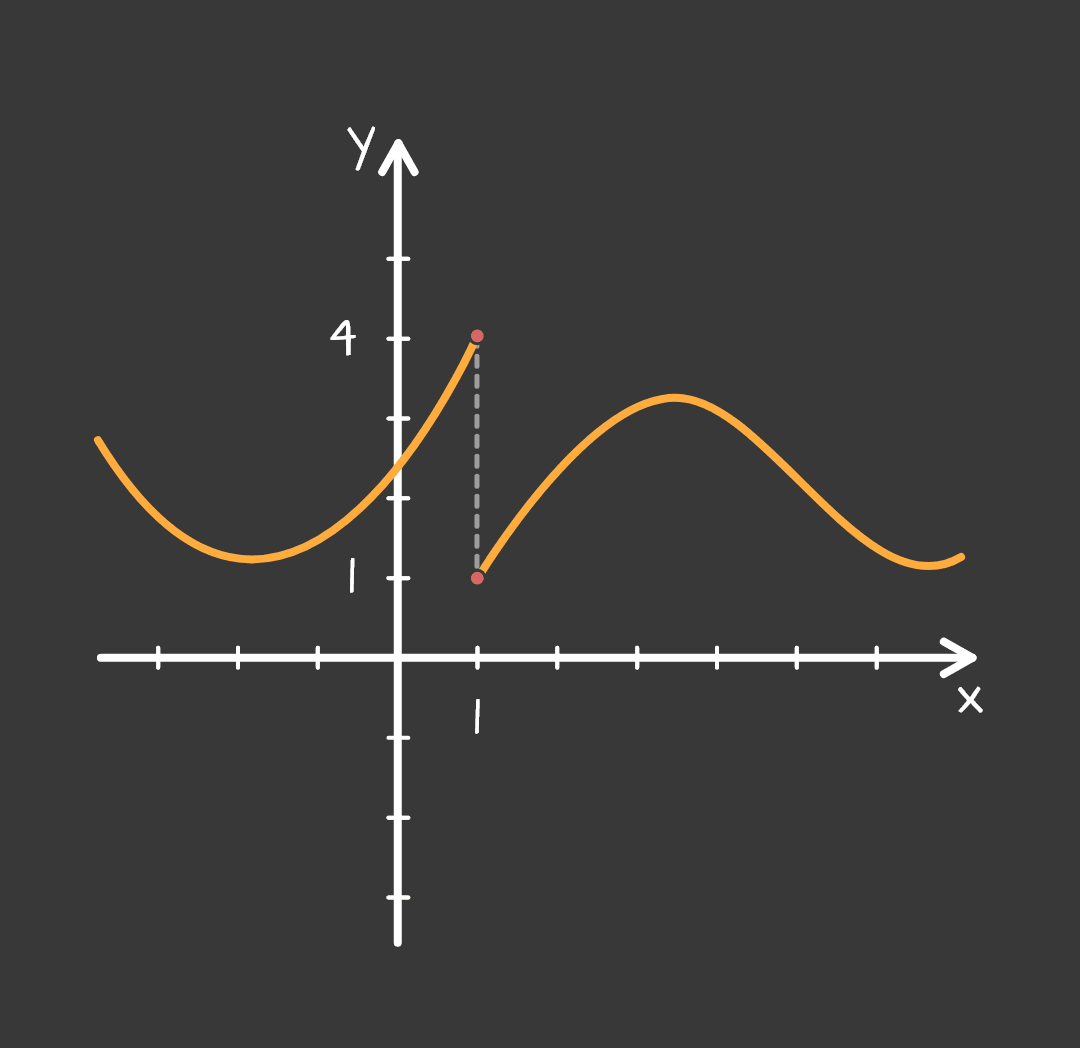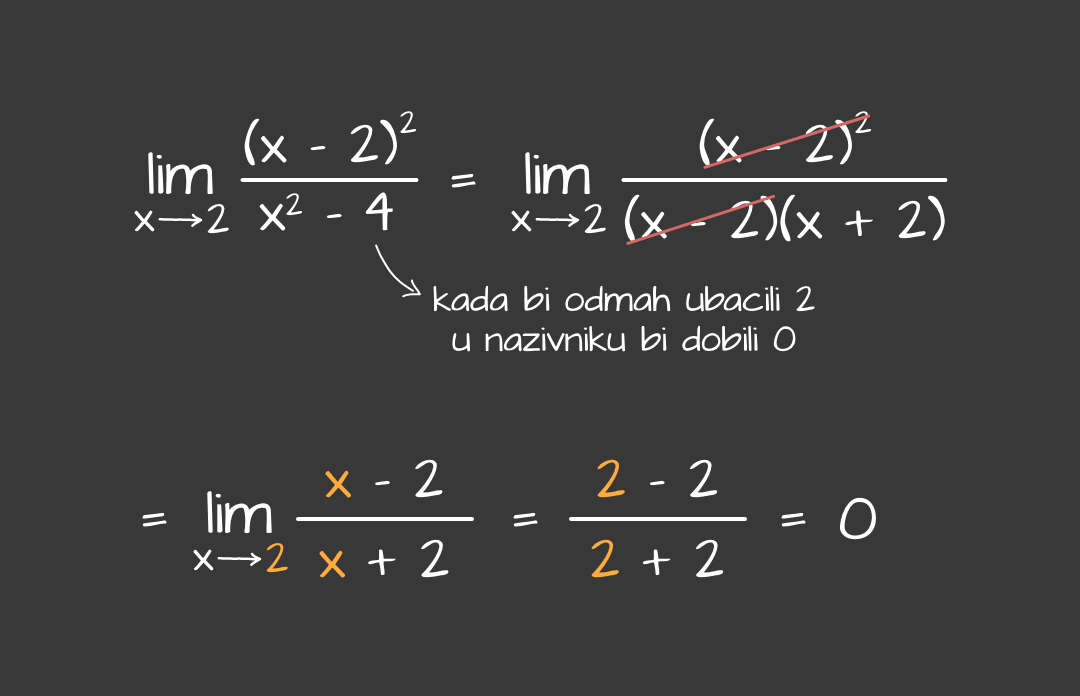Limes funkcije $f$ u beskonačnosti je broj $L$ takav da za svaki $x$ veći od nekog proizvoljno velikog broja $M$, vrijednosti funkcije $f(x)$ se nalaze u okolini, "blizu" broja $L$. Drugim riječima, što se $x$ više povećava, vrijednosti $f(x)$ su sve bliže broju $L$.
Limes funkcije u beskonačnosti$ \lim \limits_{x \rightarrow \infty} f(x)=L $

Za računanje limesa u beskončnosti često ćemo koristiti sljedeću formulu.
Limes racionalne funkcije$ \lim \limits_{x \rightarrow \infty} \frac{1}{x}=0 $
Kada god računamo limes razlomka, uvijek ćemo htjeti podijeliti i brojnik i nazivnik najvećom potencijom $x$-a i nakon toga gledati što dobijemo. Sve moguće situacije su prikazane na slici.


Limes funkcije $f$ u točki je broj $L$ takav da se okolina neke točke $c$ preslikava u okolinu točke $L$. Drugim riječima, što se $x$ više približava točki $c$, to se $f(x)$ približava $L$.
Limes funkcije u točki$ \lim \limits_{x \rightarrow c} f(x)=L $
Funkcija ima jednostrane limese, limes slijeva i limes zdesna. Oni mogu biti isti ili različiti.
Kažemo da funkcija ima limes ako postoje limes slijeva i limes zdesna te su oba jednaka.
Pogledajmo na sljedećem primjeru.

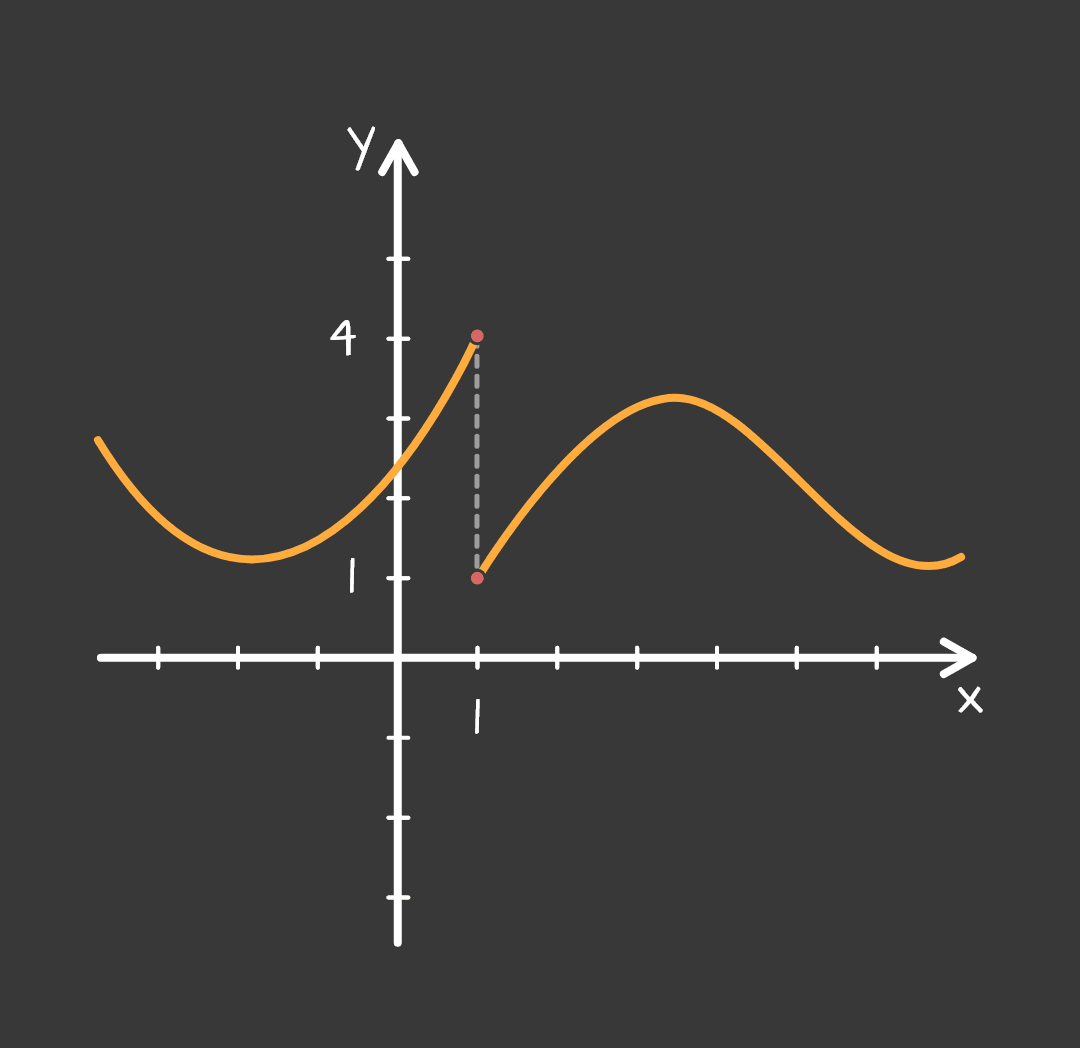
Kada se brojevi na $x$-osi s lijeve strane broja $1$ približavaju broju $1$ (pišemo $x\rightarrow 1^{-}$), tada se vrijednosti funkcije (brojevi na $y$-osi) približavaju broju $4$.
Kada se brojevi na $x$-osi s desne strane broja $1$ približavaju broju $1$ (pišemo $x\rightarrow 1^{-}$), tada se vrijednosti funkcije (brojevi na $y$-osi) približavaju broju $1$.
Kažemo da funkcija f(x) ima jednostrane limese:
- limes slijeva $ \lim_{x \to 1^{-}} f(x) = 4$
- limes zdesna $ \lim_{x \to 1^{+}} f(x) = 1$
Međutim, funkcija nema limes kada $x$ teži u $1$ jer limes slijeva i limes zdesna nisu jednaki.
Kod računanja limesa, prvo ćemo morati srediti izraz koji nam je zadan, a onda samo umjesto $x$-a uvrstiti broj prema kojem se $x$ približava.

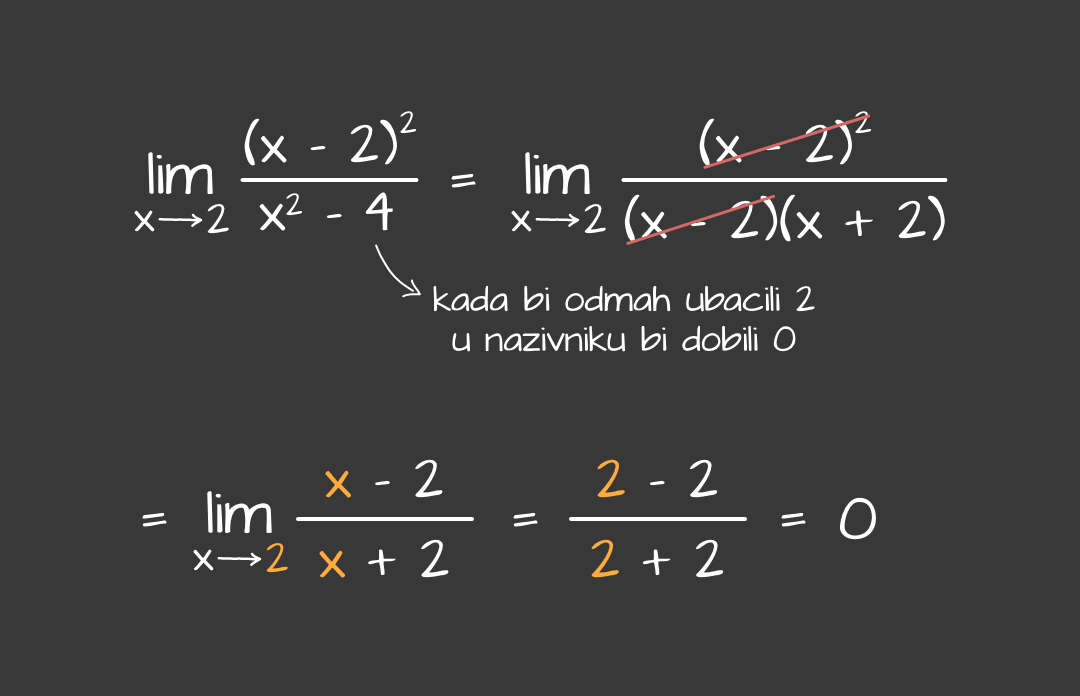
Neprekidnost funkcije
Funkcija $f$ je neprekidna u točki $c$ ako postoji limes u toj točki i on je upravo jednak vrijednosti $f(c)$.
Neprekidnost funkcije u točki$ \lim\limits_{x \rightarrow c} f(x)=f(c) $
Računanje s limesima
Kao i za računanje limesa nizova, slična pravila imamo i za limese funkcija.
Limes zbroja i razlike funkcije$ \lim \limits_{x \rightarrow a}[(f(x) \pm g(x)]=\lim \limits_{x \rightarrow a} f(x) \pm \lim \limits_{x \rightarrow a} g(x) $
Limes umnoška funkcija$ \lim \limits_{x \rightarrow a}[f(x) \cdot g(x)]=\lim \limits_{x \rightarrow a} f(x) \cdot \lim \limits_{x \rightarrow a} g(x) $
Limes razlomka funkcija$ \lim \limits_{x \rightarrow a} \frac{f(x)}{g(x)}=\frac{\lim \limits_{x \rightarrow a} f(x)}{\lim \limits_{x \rightarrow a} g(x)} $
Limes potencije funkcije$ \lim \limits_{x \rightarrow a} f(x)^{g(x)}=\lim \limits_{x \rightarrow a} f(x)^{\lim \limits_{x \rightarrow a} g(x)} $