Pojam funkcije

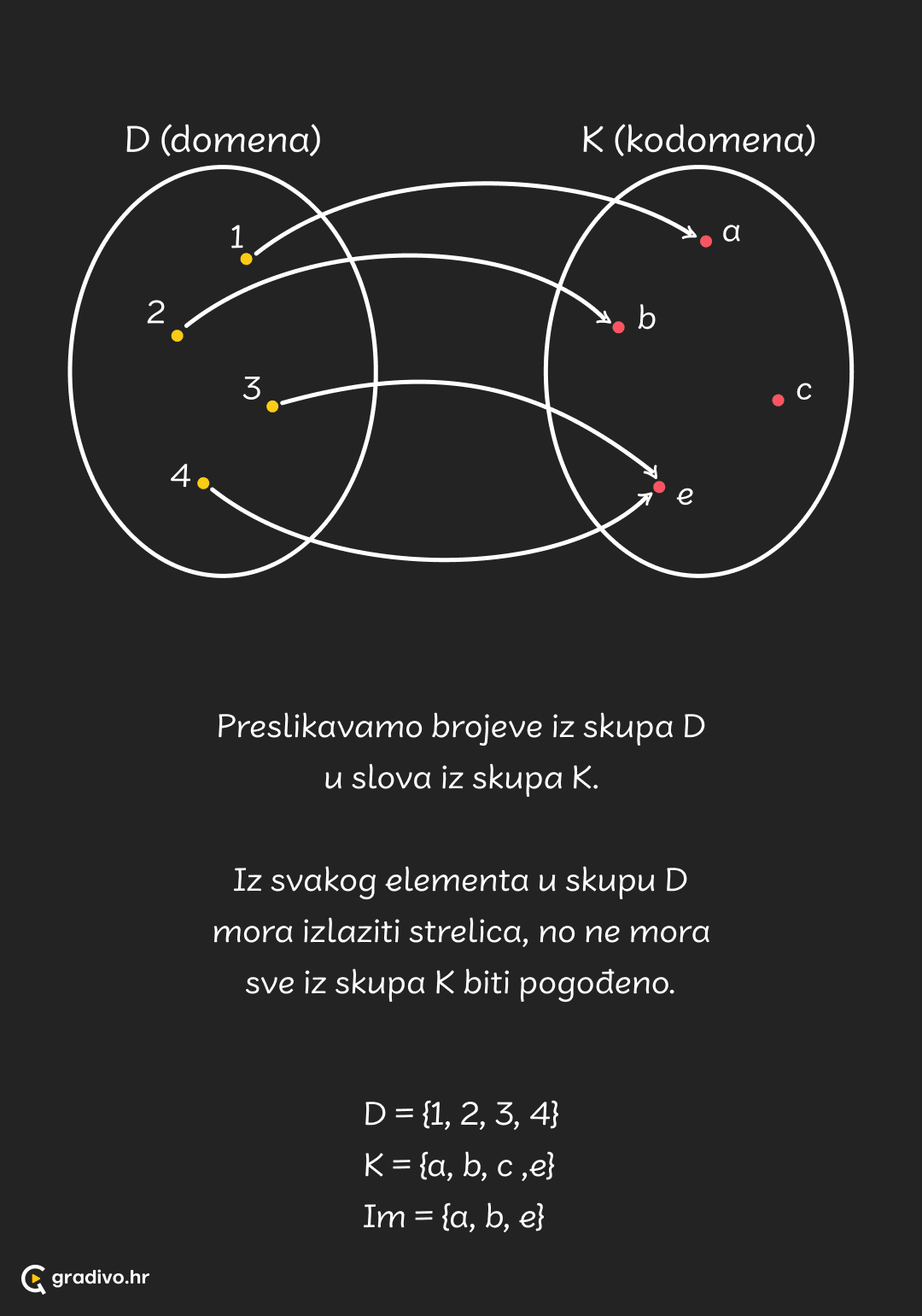
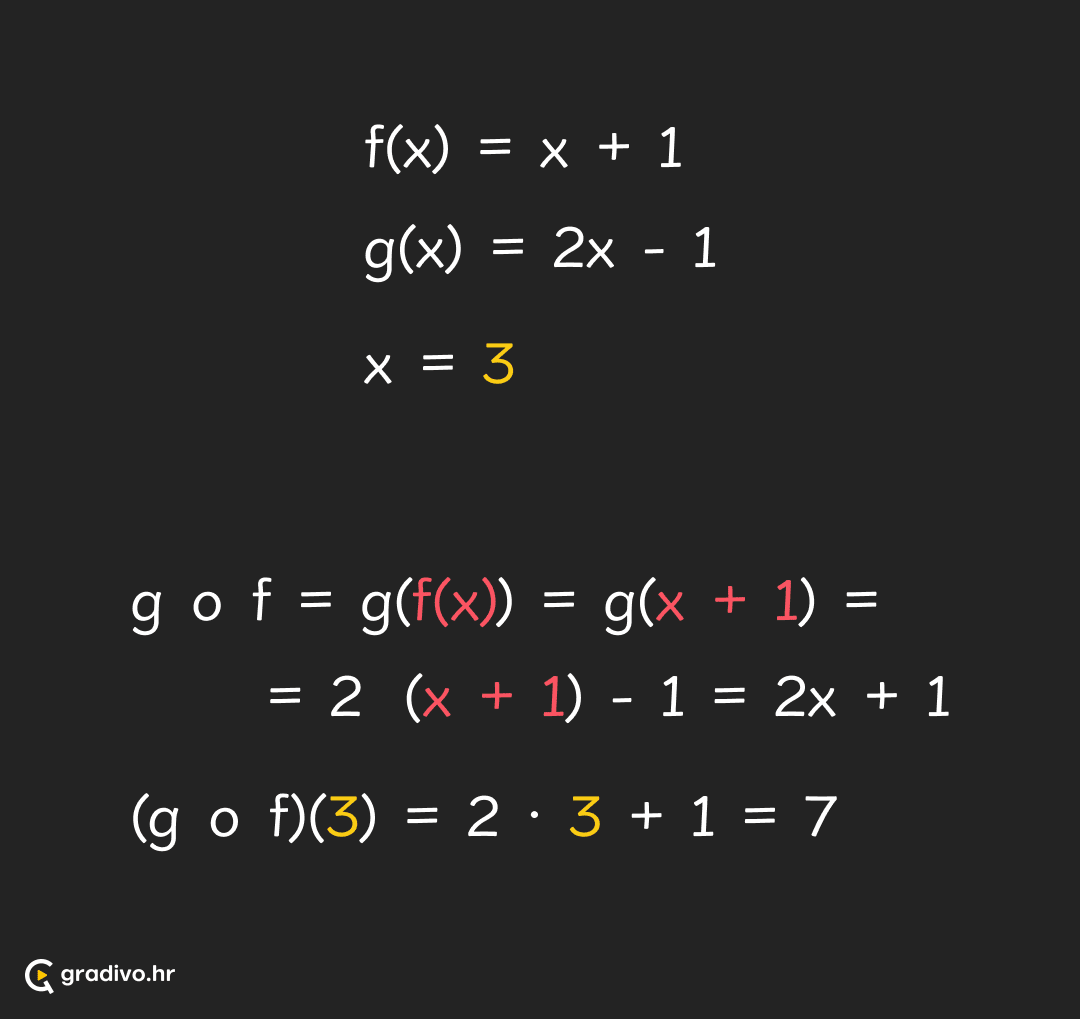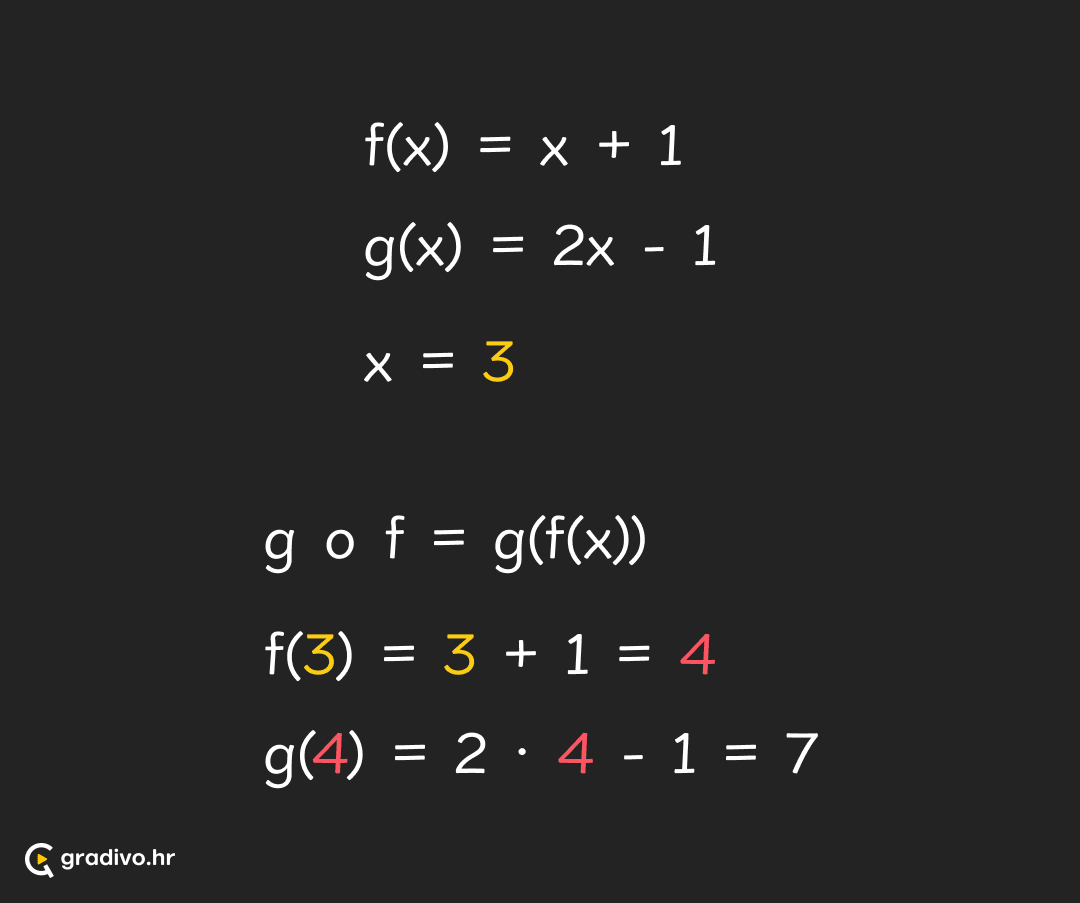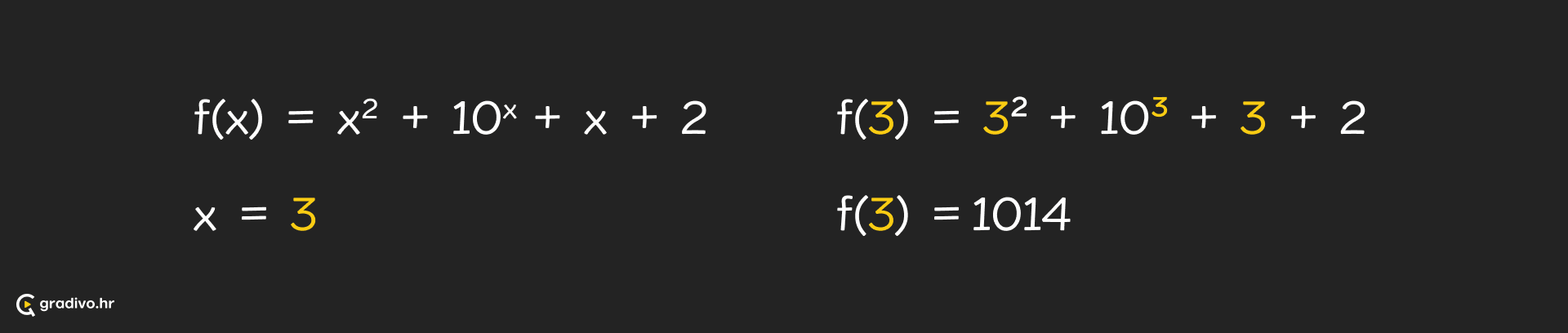Funkcija je pridruživanje, preslikavanje elemenata iz jednog skupa u drugi. Bitno je da svakom elementu prvog skupa pridružimo točno jedan element drugog skupa - inače nije funkcija.

Funkciju također možemo zamisliti i kao "crnu kutiju" u koju nešto ubacimo, a onda nam ona po nekom pravilu izbaci nešto van.

Graf funkcije je ono što dobijemo kada funkciju nacrtamo u koordinatnom sustavu. Formalno, to je skup točaka $(x,f(x))$, za sve $x$ koje funkcija može primiti.

Je li neki graf funkcija možemo provjeriti vertikalnim testom. Ako vertikalni pravac siječe funkciju u dvije ili više točaka, nije funkcija, a u suprotnom jest.

Funkciju označavamo s $f: D \rightarrow K$, gdje je $f$ ime same funkcije, $D$ onaj prvi skup iz kojeg uzimamo elemente, a $K$ je skup gdje se nalaze sve moguće vrijednosti koje funkcija može vratiti.

Skup $D$ se zove domena (područje definicije), a $K$ je kodomena (područje vrijednosti). Elemente domene, što je najčešće naš $x$, zovemo argument (nezavisna varijabla) funkcije, a elemente kodomene $y$ vrijednosti (zavisne varijable) funkcije.

Slika funkcije je skup svih mogućih vrijednosti koje funkcija može poprimiti. Ne mora nužno biti isto što i kodomena. Kodomena može sadržavati još neke elemente koje funkcija nikad neće pogoditi. Oznaka za sliku je $Im$.

Domena i slika funkcije

Pogledajmo kako se određuju domena i slika funkcije ako ju imamo nacrtano u koordinatnom sustavu.

Domenu gledamo na $x$-osi, odnosno koji su to sve $x$-evi koji će davati neku vrijednost funkcije. Npr. logaritamska funkcija na prvoj slici, ne izbacuje nikakvu vrijednost za $x=-1$ jer iznad tog $x$-a nema ničega. Ali recimo za $x=2$, vidimo da je iznad njega točno jedna točka pa je on u domeni.

Sliku određujemo na isti način, samo gledamo po $y$-osi. Dakle pitamo se, koji su to sve $y$-i koje funkcija može postići? Zamislimo si kao da spljoštimo graf na $y$-os i pogledamo što je sve taj graf pogodio. To će nam upravo biti slika. Za domenu smo mogli razmišljati na isti način, samo bi graf morali spljoštiti na $x$-os.

Postoje tri pravila za određivanje domene funkcije, ovisno o kojoj se funkciji radi.

• ako u funkciji imamo razlomak, bitno je da nazivnik bude različit od $0$
• ako u funkciji imamo korijen, bitno je da veličina pod korijenom bude veća ili jednaka $0$
• ako u funkciji imamo logaritam, moramo paziti na dvije stvari:
  1) baza logaritma mora biti veća od $0$ i različita od $1$
  2) veličina pod logaritmom mora biti veća od $0$

Injekcija, surjekcija i bijekcija

Funkcija je injekcija ako se svaki $x$ preslika u svoj, drugačiji $y$ tj. ako ne postoje dva $x$-a za koja će funkcija izbaciti istu vrijednost. Injektivnost se provjerava horizontalnim testom. Slično kao i vertikalni test, ako vodoravni pravac siječe funkciju u dvije ili više točke, nije injekcija, a u suprotnom jest.

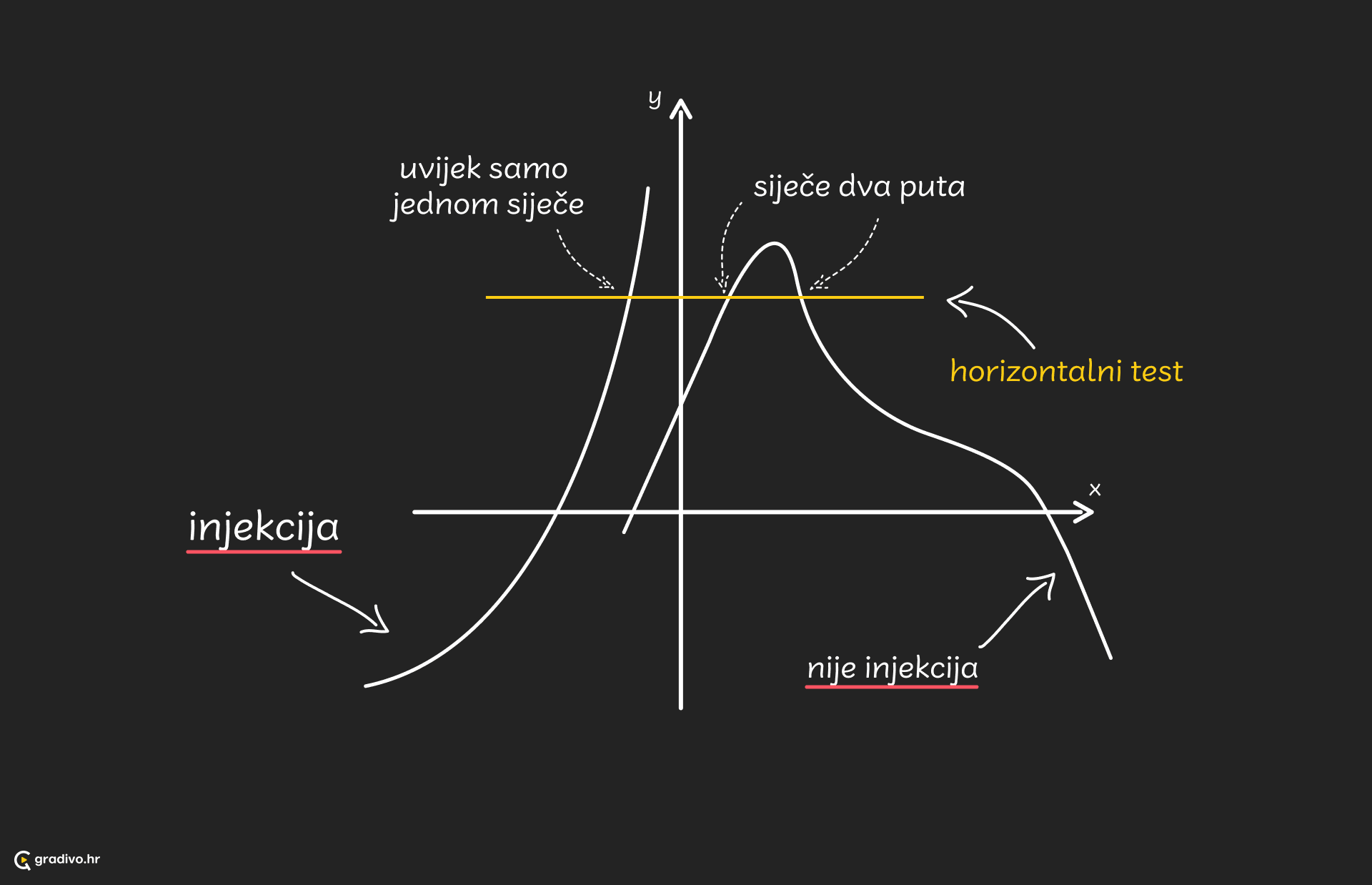
Funkcija je surjekcija ako je slika funkcije jednaka kodomeni funkcije. Drugim riječima, ako je svaki element kodomene pogođen.

Funkcija je bijekcija ako je injekcija i surjekcija.

Vrijednost funkcije

Kada želimo izračunati vrijednost neke funkcije u nekoj točki $x$, sve što trebamo napraviti je zamijeniti svako pojavljivanje varijable $x$ u funkciji s brojem koji mu je pridružen. Izraz koji dobijemo bi trebao imati samo brojeve, njega izračunamo i rezultat će biti ono što zovemo vrijednost funkcije.

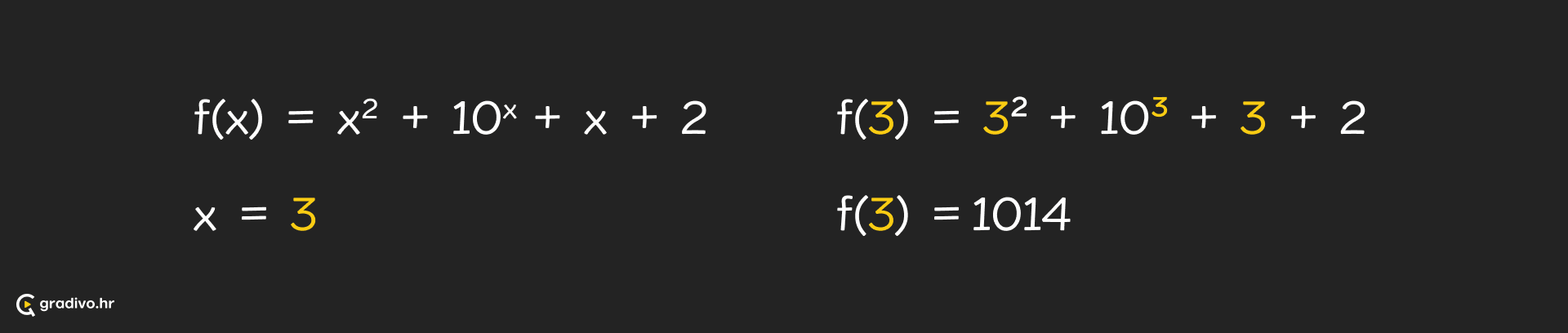
Kompozicija funkcija

Kompozicija funkcija je operacija među funkcijama koja označava djelovanje jedne funkcije na drugu. Preciznije, jedna funkcija djeluje normalno, kao što smo navikli, na argument $x$, a druga funkcija djeluje na rezultat koji izbaci prva funkcija za taj $x$.

Za funkcije $f$ i $g$, kompozicija funkcija $f$ i $g$ se označava s $g \circ f$.

Kompoziciju možemo računati na dva načina. Prvi je da izračunamo kako izgleda baš funkcija koja je nastala kao kompozicija, a onda uvrstimo broj koji nas zanima. U drugom načinu prvo izračunamo vrijednost unutarnje funkcije u broju koji je zadan, a onda za dobivenu vrijednost izračunamo vrijednost druge, vanjske funkcije.

Oprez! $g \circ f \neq f \circ g$

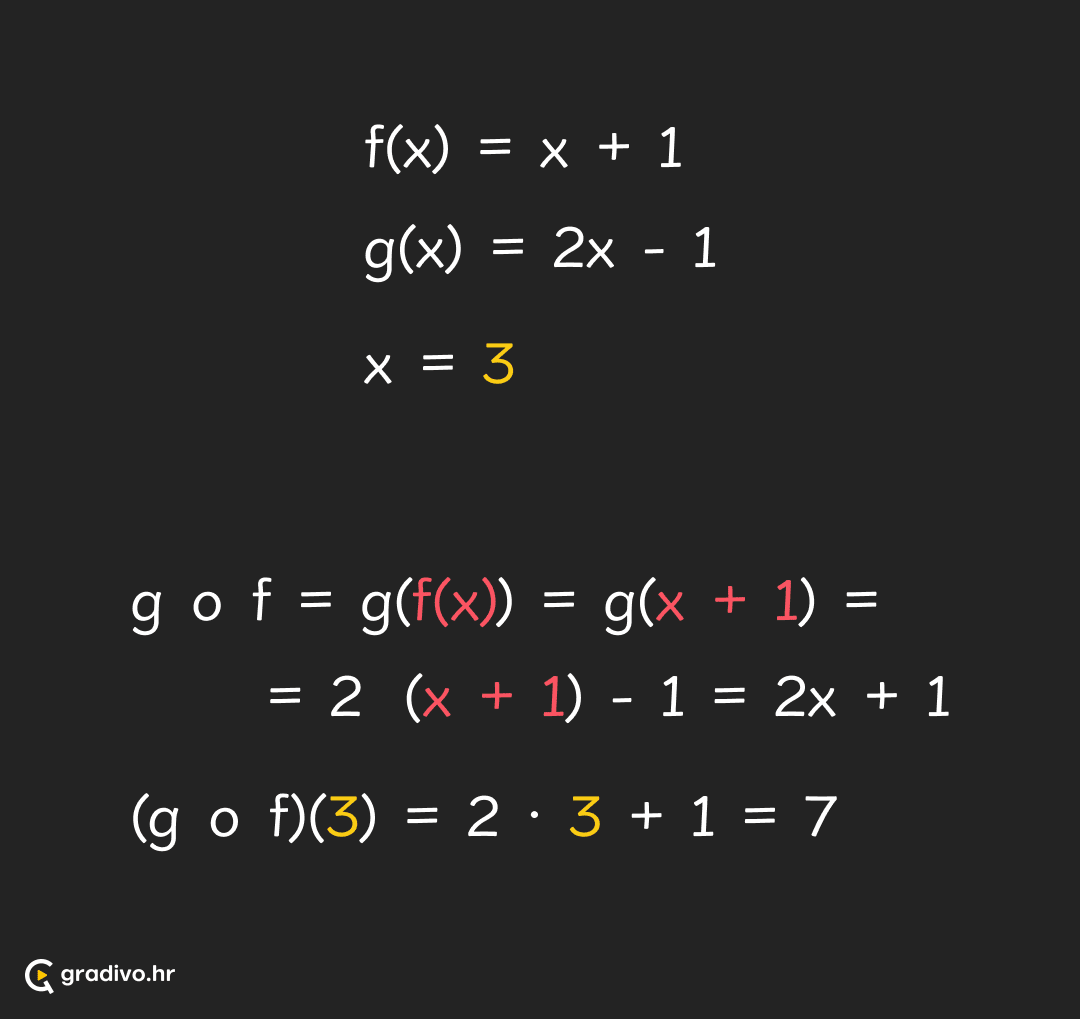
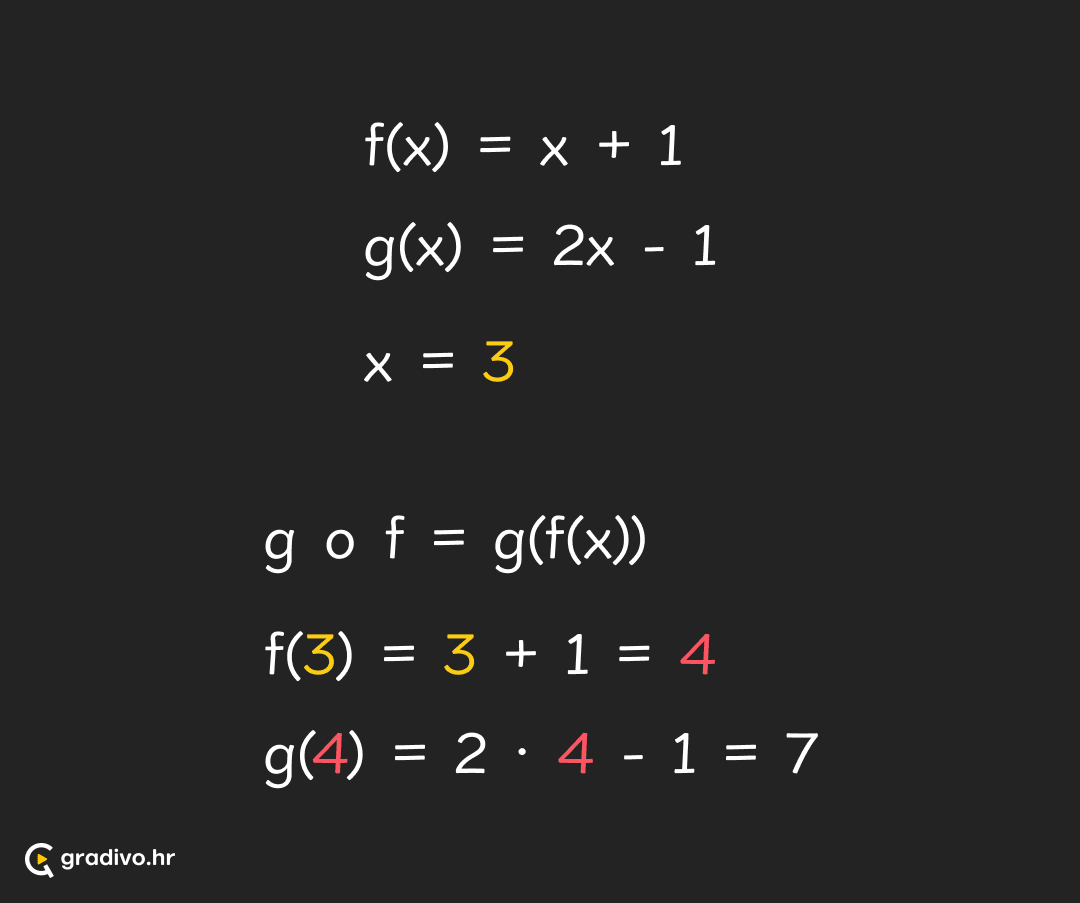
Inverzna funkcija

Funkcije $g$ inverzna je funkciji $f$ ako vrijedi:

• $g(f(x))=x$ za svaki $x \in D_f$
• $f(g(y))=y$ za svaki $y \in D_g$.

Pišemo $g=f^{-1}$. U isto vrijeme je funkcija $f$ inverzna funkciji $g$ te pišemo $f=g^{-1}$.

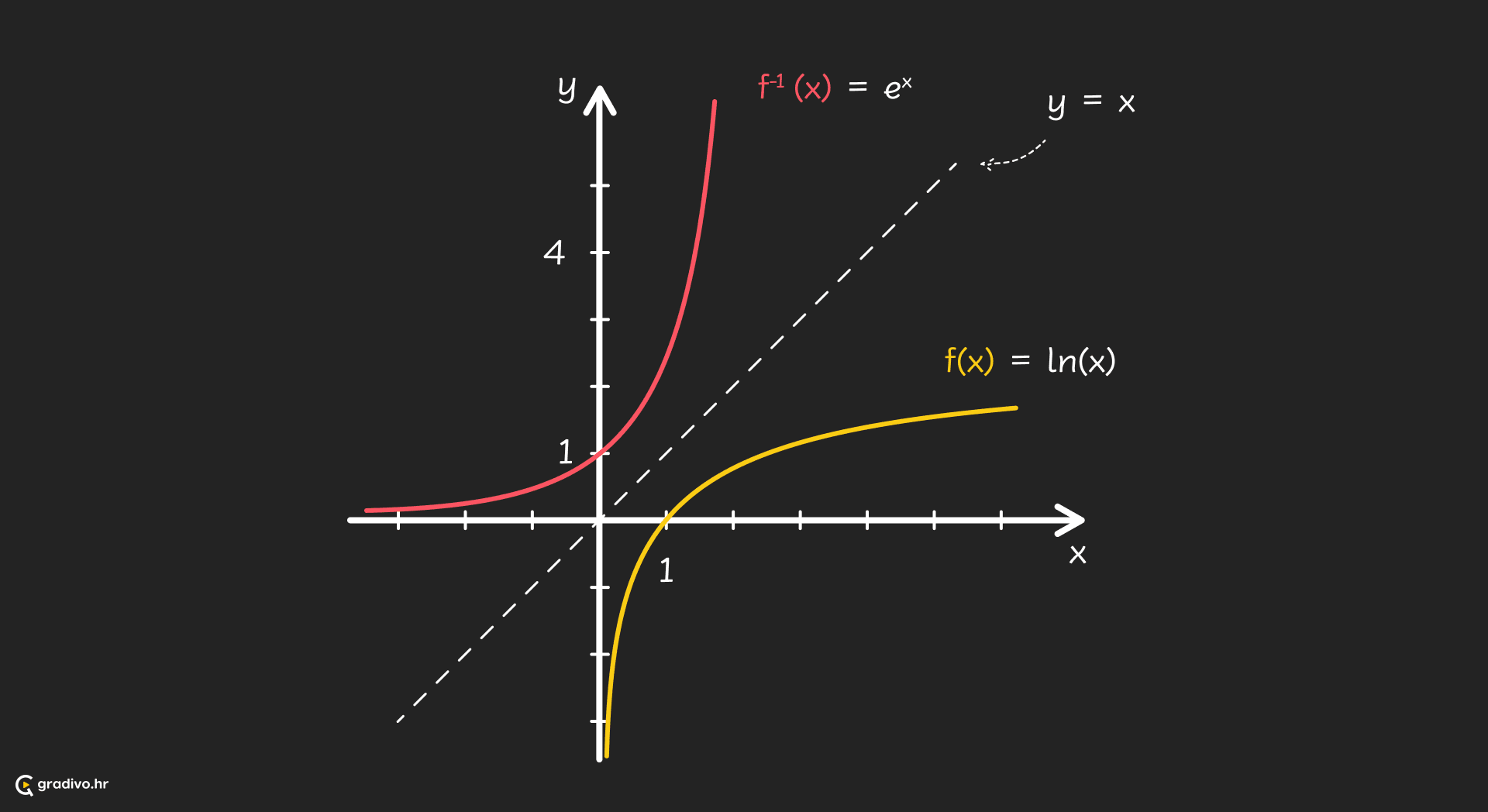
Grafovi inverznih funkcija $f$ i $g$ simetrični su s obzirom na pravac $y=x$.

Postupak za traženje inverzne funkcije funkciji $f(x)$:

1. zapišemo $y=f(x)$
2. jednadžbu $y=f(x)$ riješimo po nepoznanici $x$
3. ako postoji jedinstveno rješenje te jednadžbe, tada je inverzna funkcija $x=f^{-1}(y)$
4. na kraju samo zamijenimo imena nepoznanica, gdje piše $x$ stavit ćemo $y$ i obrnuto te dobijemo zapis $y=f^{-1}(x)$

Napomena: Funkcija ima inverznu funkciju onda i samo onda ako je ona bijekcija.