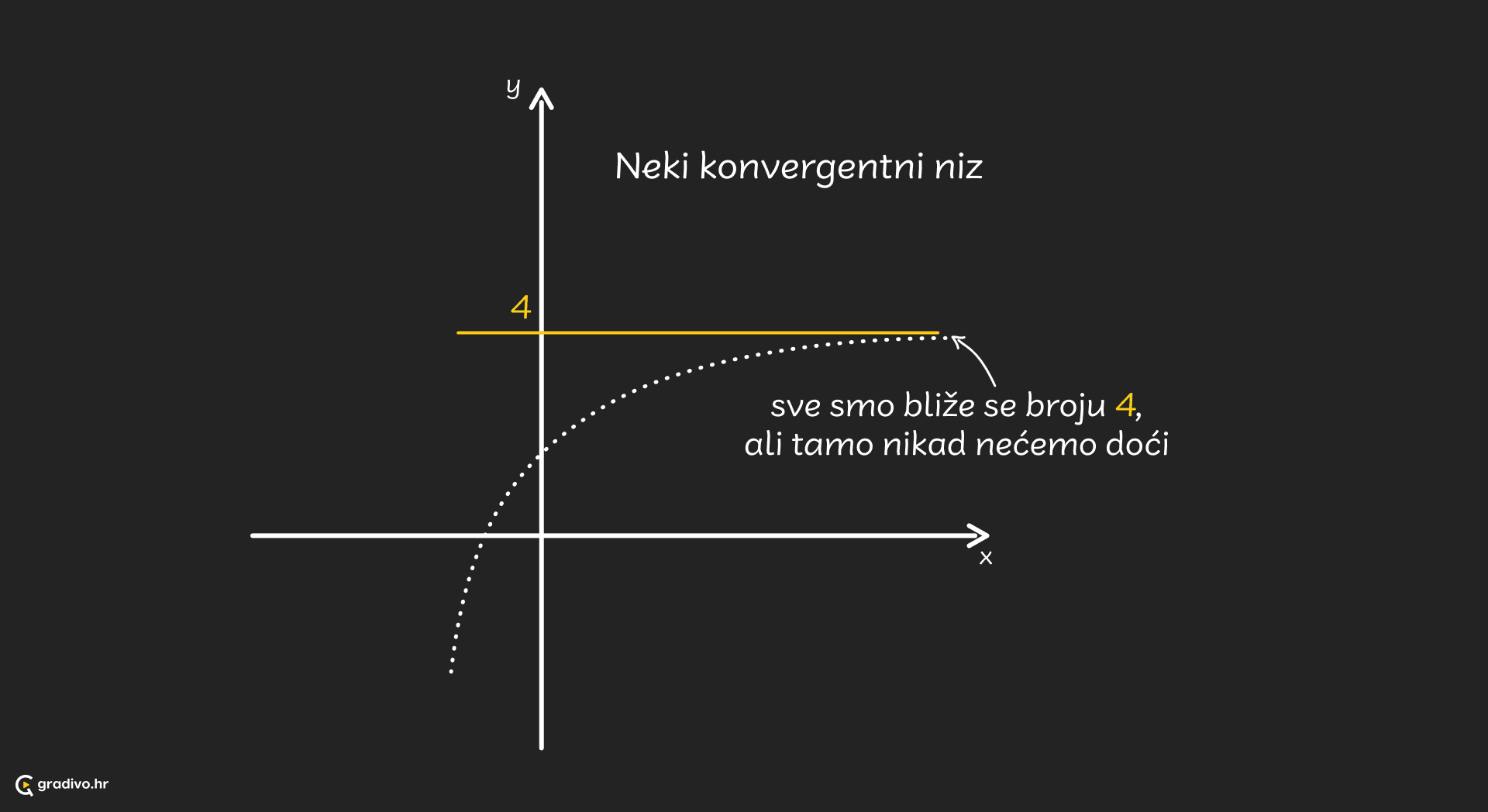
Limes (granična vrijednost), označimo ga s $L$, je broj oko kojeg se nalazi beskonačno mnogo članova nekog niza $a_n$. Drugim riječima, bez obzira koliko se malo udaljimo od $L$, koliko malu okolinu gledamo, uvijek će u njoj biti beskonačno puno članova niza. Zapišimo oznaku za limes. Čitamo: "limes niza $a_n$ je $L$, kada $n$ teži (ide, pustimo) u beskonačnost".
$ \lim \limits_{x \rightarrow \infty} a_{n}=L $
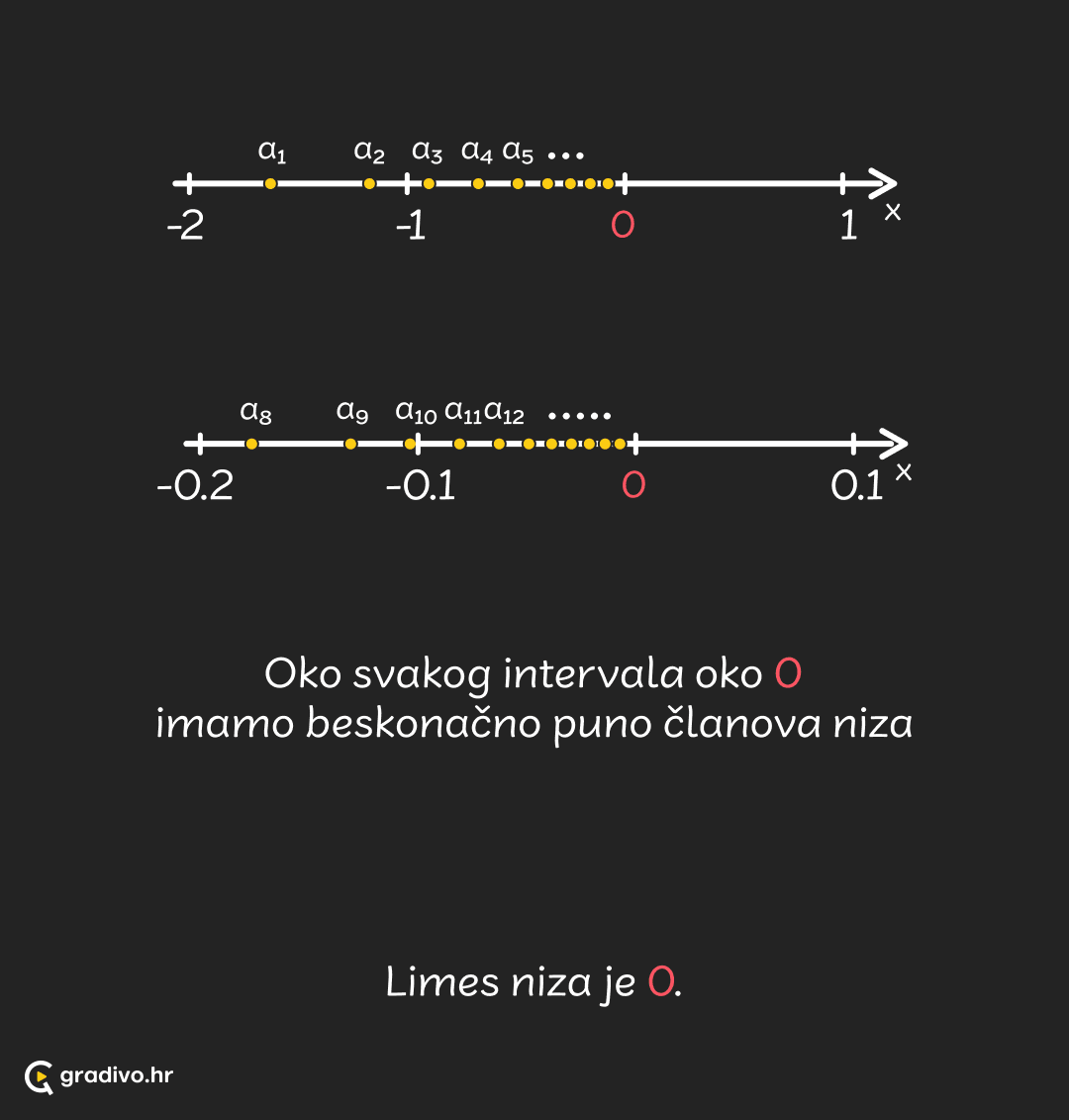
Ako niz $a_n$ ima limes, onda je taj niz konvergentan, i konvergira prema $L$.
Ako niz $a_n$ nema limes, onda je taj niz divergentan.
Limes koji teži u beskonačnosti
Niz $(a_n)$ teži u beskonačnost ako za bilo koji broj, bez obzira koliko velik, postoji beskonačno mnogo članova niza koji su veći od njega.
Slično, teži u minus beskonačno ako za proizvoljno mali broj možemo naći beskonačno puno članova niza koji su još manji od njega.
$ \lim \limits_{x \rightarrow \infty} a_{n}= \pm \infty $
Za niz kažemo da je konstantan ako su mu svi članovi isti. Niz $(a_n)$ gdje je $a_n$ uvijek jednak nekom broju $c$ ima limes i $\lim \limits_{x \rightarrow \infty} a_n= \lim \limits_{x \rightarrow \infty} c=c$.
Za aritmetički niz $(a_n)$ s razlikom $d>0$ vrijedi $\lim \limits_{x \rightarrow \infty} a_{n}=\infty$.
Ako je $d<0$, onda je $\lim \limits_{x \rightarrow \infty} a_{n}=-\infty$.
Za geometrijski niz $(a_n)$ s kvocijentom $|q|<1$ vrijedi $\lim _{n \rightarrow \infty} a_{n}=0$.
Ako je $q>1$, niz je divergentan, tj. $\lim \limits_{x \rightarrow \infty} a_{n}=\infty$.
Ako je $q \leq -1$ limes ne postoji.
Ako je $q=1$, niz je konstantan pa i konvergentan.
$ \text{Ako }\lim \limits_{x \rightarrow \infty} a_{n}=\infty, \text { onda je } \lim \limits_{x \rightarrow \infty} \frac{1}{a_{n}}=0 $
$ \lim \limits_{x \rightarrow \infty}\left(a_{n} \pm b_{n}\right)=\lim \limits_{x \rightarrow \infty} a_{n} \pm \lim \limits_{x \rightarrow \infty} b_{n} $
$ \lim \limits_{x \rightarrow \infty} (c \cdot b_{n})=c \cdot \lim \limits_{x \rightarrow \infty} b_{n} $
$ \lim \limits_{x \rightarrow \infty}\left(a_{n} \cdot b_{n}\right)=\lim \limits_{x \rightarrow \infty} a_{n} \cdot \lim \limits_{x \rightarrow \infty} b_{n} $
$ \lim \limits_{x \rightarrow \infty} \frac{a_{n}}{b_{n}}=\frac{\lim \limits_{x \rightarrow \infty} a_{n}}{\lim \limits_{x \rightarrow \infty} b_{n}} $
