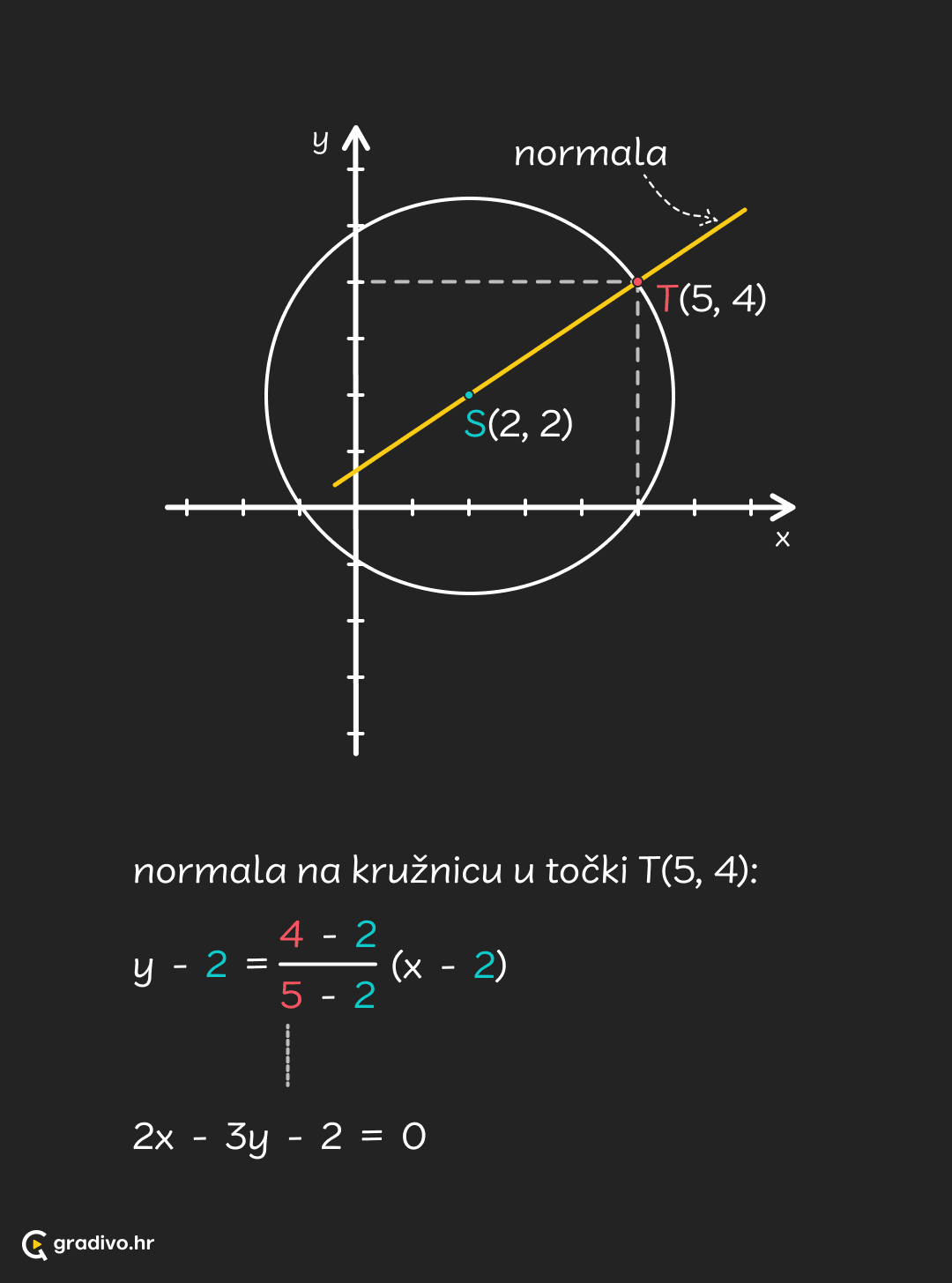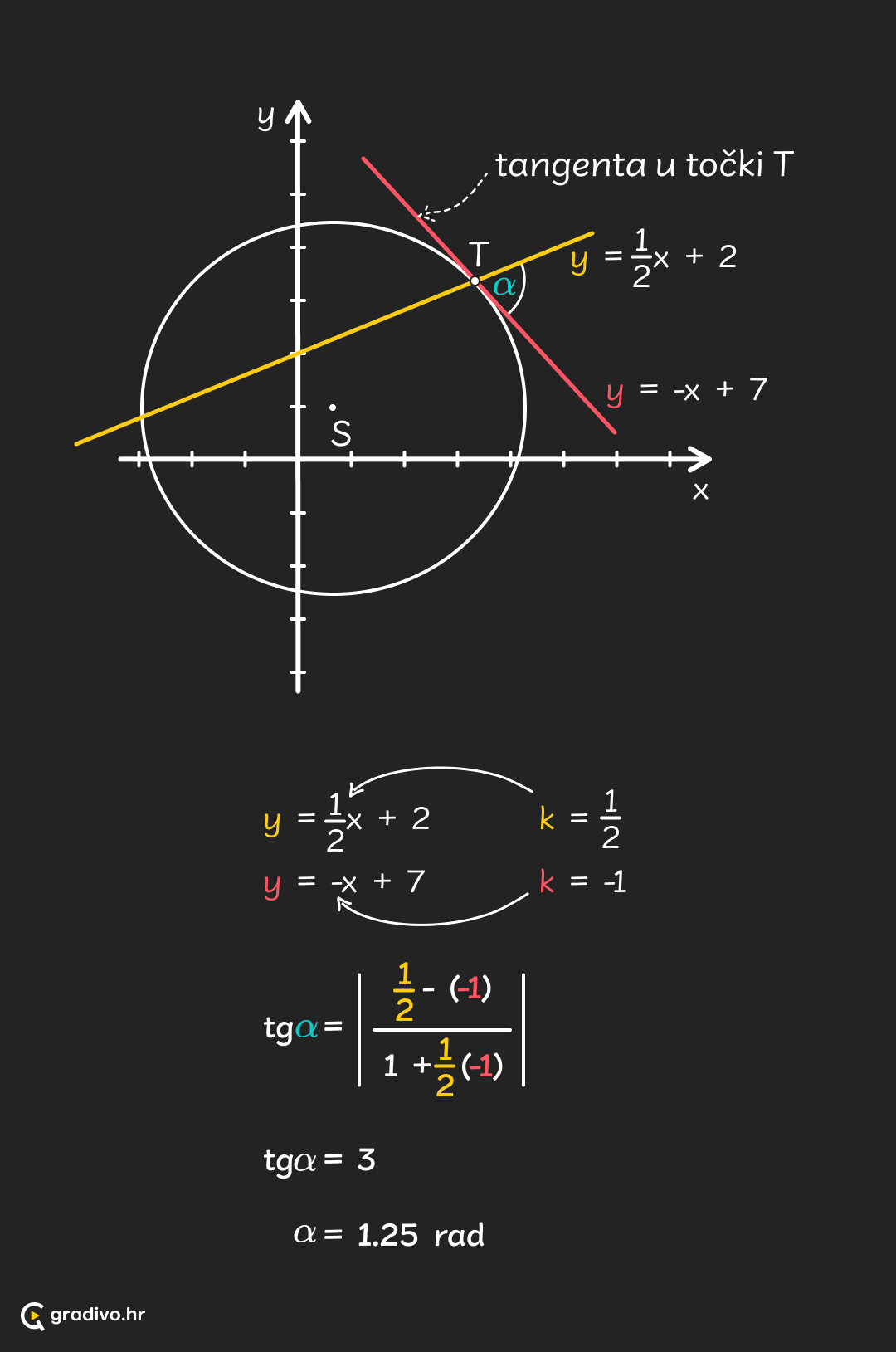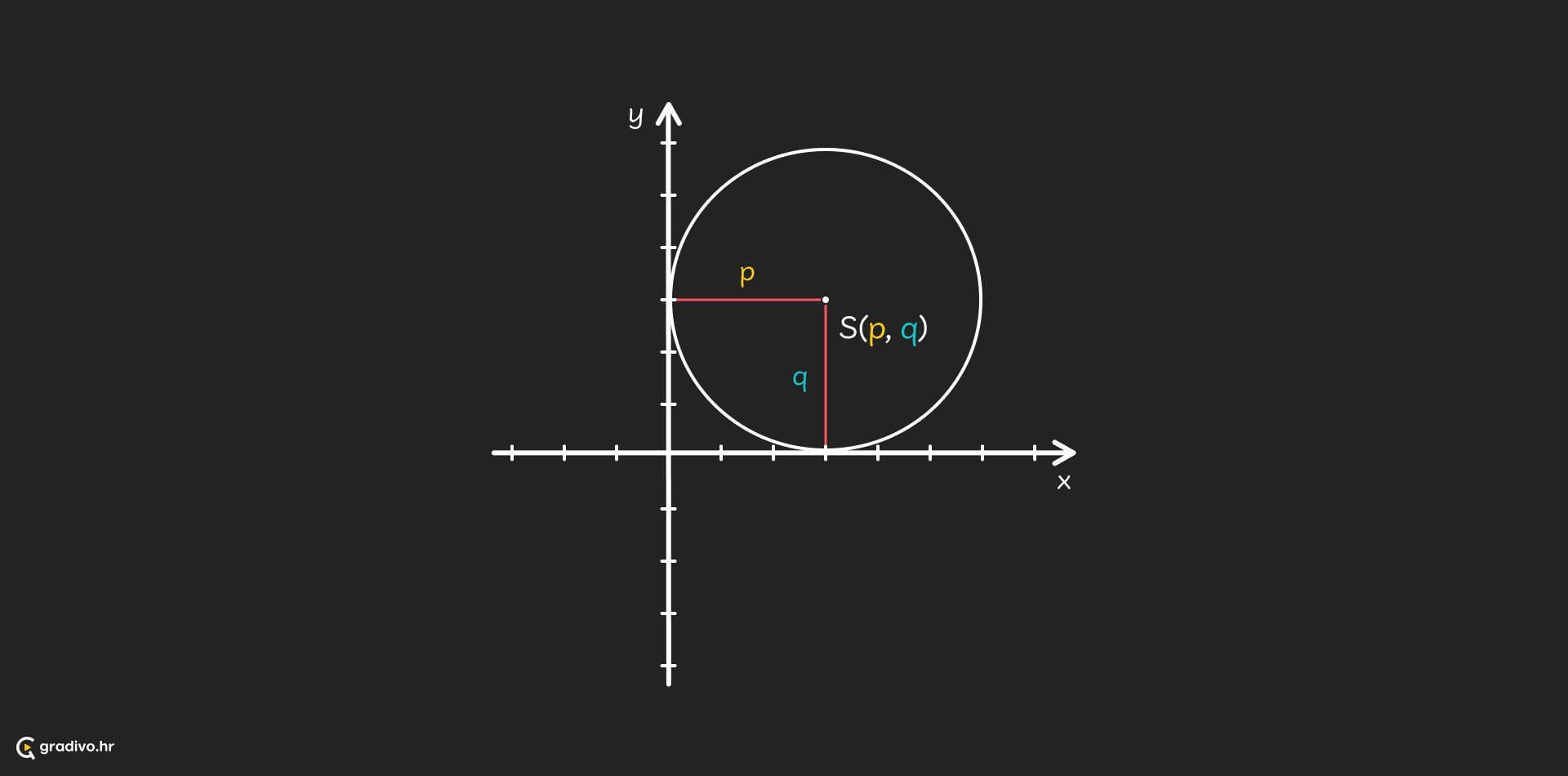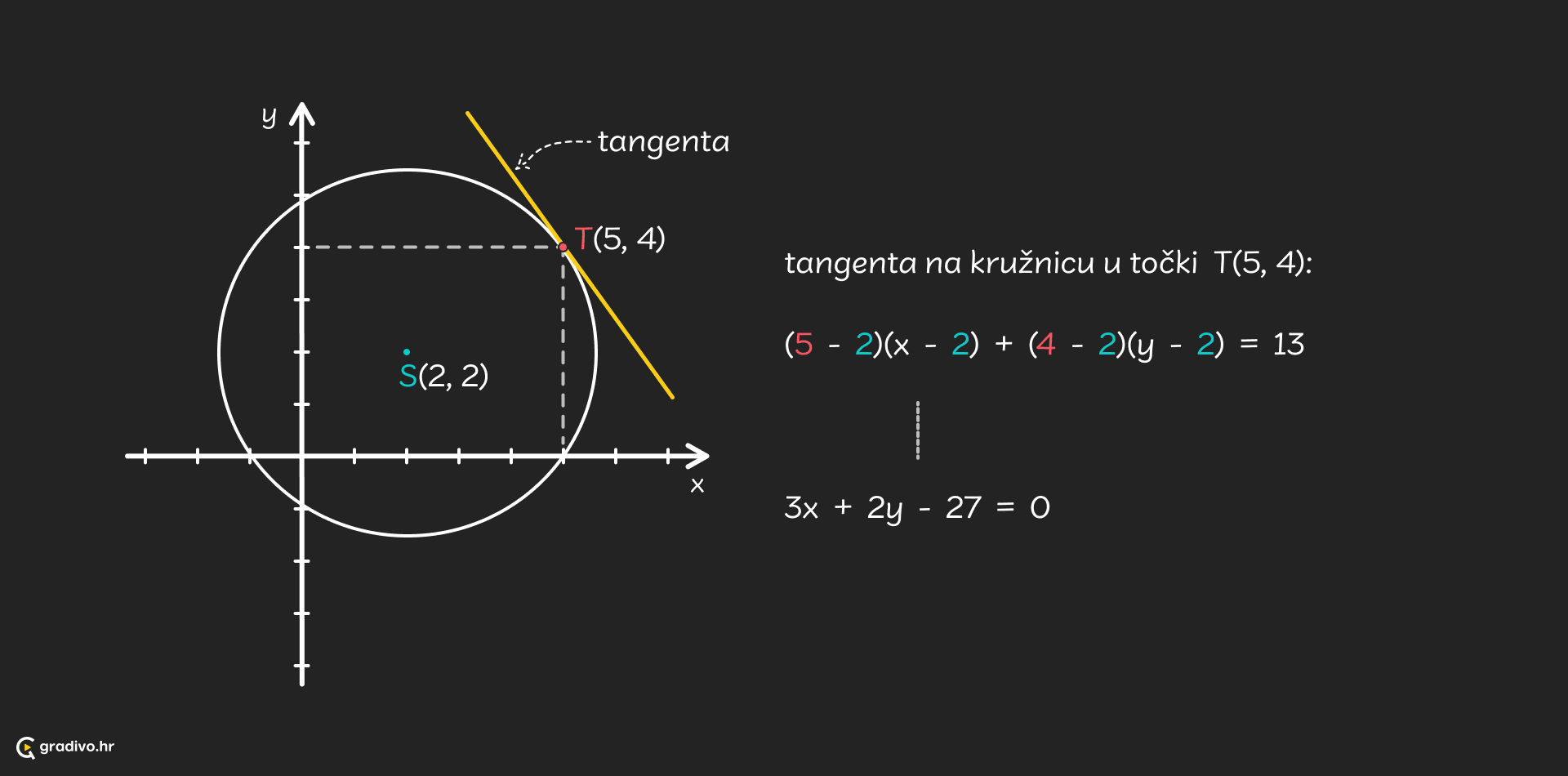2 + 1 GRATIS na pripreme za maturu do kraja rujna!

11d 9h 40m 53s

Kružnice u koordinatnom sustavu

Matematika A3. razred
Besplatne materijale donosi ti Cedevita Logo

Na prošloj stranici smo već rekli kako izgledaju jednadžbe kružnica sa središtem u $S(p,q)$ i sa središtem u ishodištu $S(0,0)$ radijusa $r$. Evo jednadžbi još jednom.

$ (x-p)^{2}+(y-q)^{2}=r^{2} $
Jednadžba kružnice sa središtem u S(p,q)
$ x^{2}+y^{2}=r^{2} $
Jednadžba kružnice sa središtem u S(0,0)

Kružnice u posebnom položaju

Koncentrične kružnice su kružnice s istim središtem, ali različitim polumjerima.

Koncentricne_kruznice_-_mobiled0049f014cc807d991d9a3f82ebcc055598100a6

Kružnice koje diraju koordinatne osi. Ako kružnica dira os $x$ tada je $q=r$. Ako kružnica dira os $y$ tada je $p=r$.

U slučaju kada kružnica dira obje koordinatne osi bit će $p=q=r$.

Tangente koordinatne osi - mobile (1)

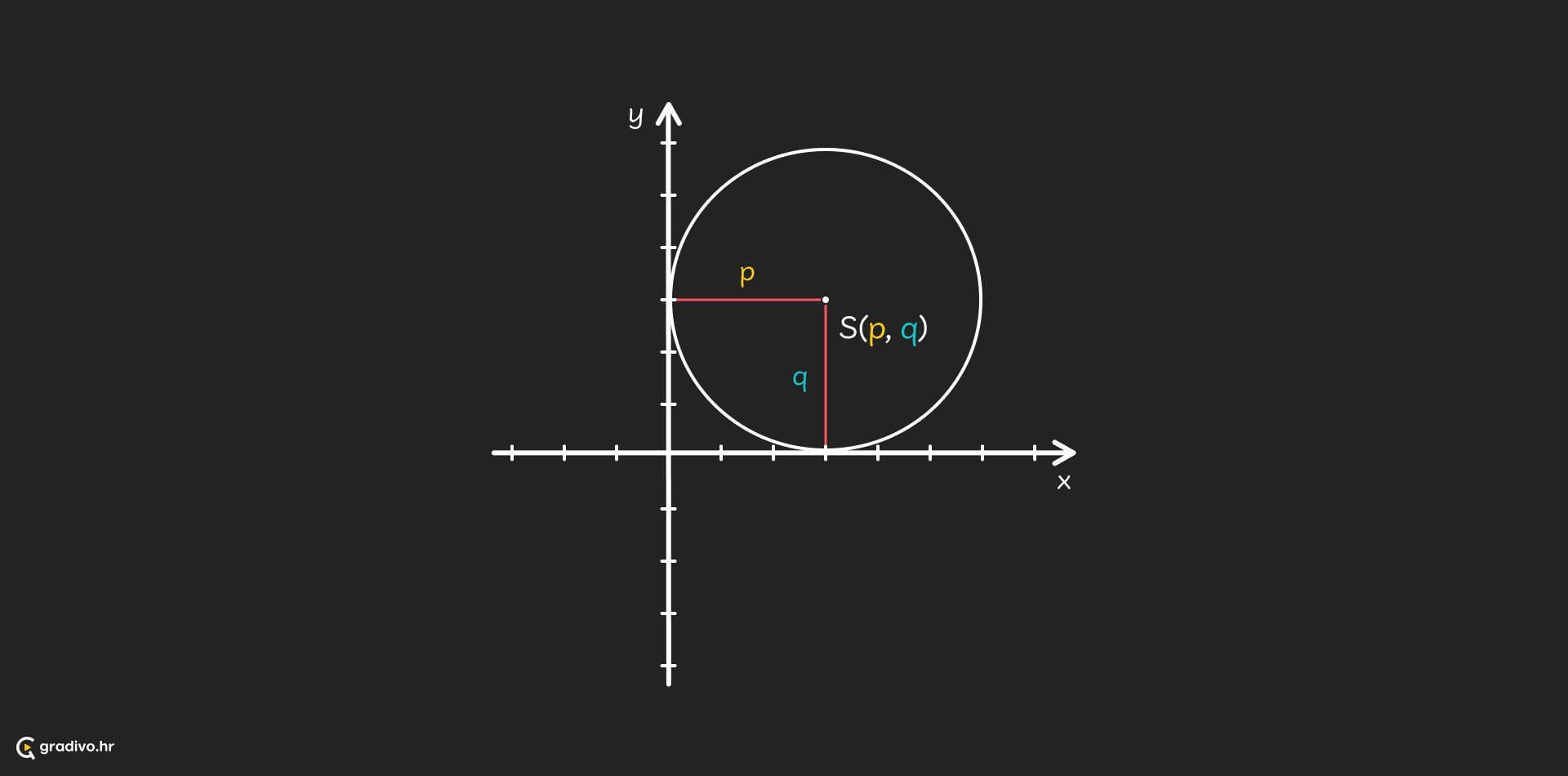
Kružnica kroz tri točke

Ako su imamo tri točke u koordinatnom sustavu, postoji točno jedna kružnica koja prolazi kroz sve njih. Do njezine jednadžbe ćemo doći tako da u opću jednadžbu kružnice (prva formula na stranici) ubacimo umjesto $x$ i $y$ koordinate zadanih točaka.

Na taj način dobijemo sustav tri jednadžbe s tri nepoznanice. Uvijek ga lagano možemo pojednostaviti tako da dva puta oduzmemo po dvije jednadžbe. Npr. od prve jednadžbe prvo oduzmemo drugu, a zatim i treću jednadžbu. To se radi tako da se lijeve strane obje jednadžbe oduzmu, a onda i desne. Na ovaj način dobijemo dvije jednadžbe s dvije nepoznanice od kuda ćemo dobiti $p$ i $q$, a $r$ dobijemo kada u bilo koju jednadžbu ubacimo upravo izračunate $p$ i $q$.

Kružnica i pravac

Kružnica i pravac mogu se:

  • sjeći u dvije točke ($d<r$, $d$ je udaljenost središta kružnice od pravca)
  • dirati se u jednoj točki ($d=r$)
  • uopće ne sjeći ($d>r$)

Do sjecišta kružnice i pravca (ako ih imamo) dolazimo rješavanjem sustava jednadžbi koji čine jednadžba kružnice i jednadžba pravca.

Uvjet dodira pravca i kružnice. Pravac $y=kx+l$ dira kružnicu $(x-p)^{2}+(y-q)^{2}=r^{2}$ ako vrijedi:

$ r^{2}\left(1+k^{2}\right)=(q-k p-l)^{2} $
Uvjet dodira pravca i kružnice

Tangenta na kružnicu. Jednadžba tangente u točki $T(x_0,y_0)$ na kružnicu je:

$ \left(x_{0}-p\right)(x-p)+\left(y_{0}-q\right)(y-q)=r^{2} $
Tangenta na kružnicu u točki $T(x_0,y_0)$
Tangenta_i_normala_-_mobile4b382435ade5aa6f9eb1b802ed911b40b913dc0e

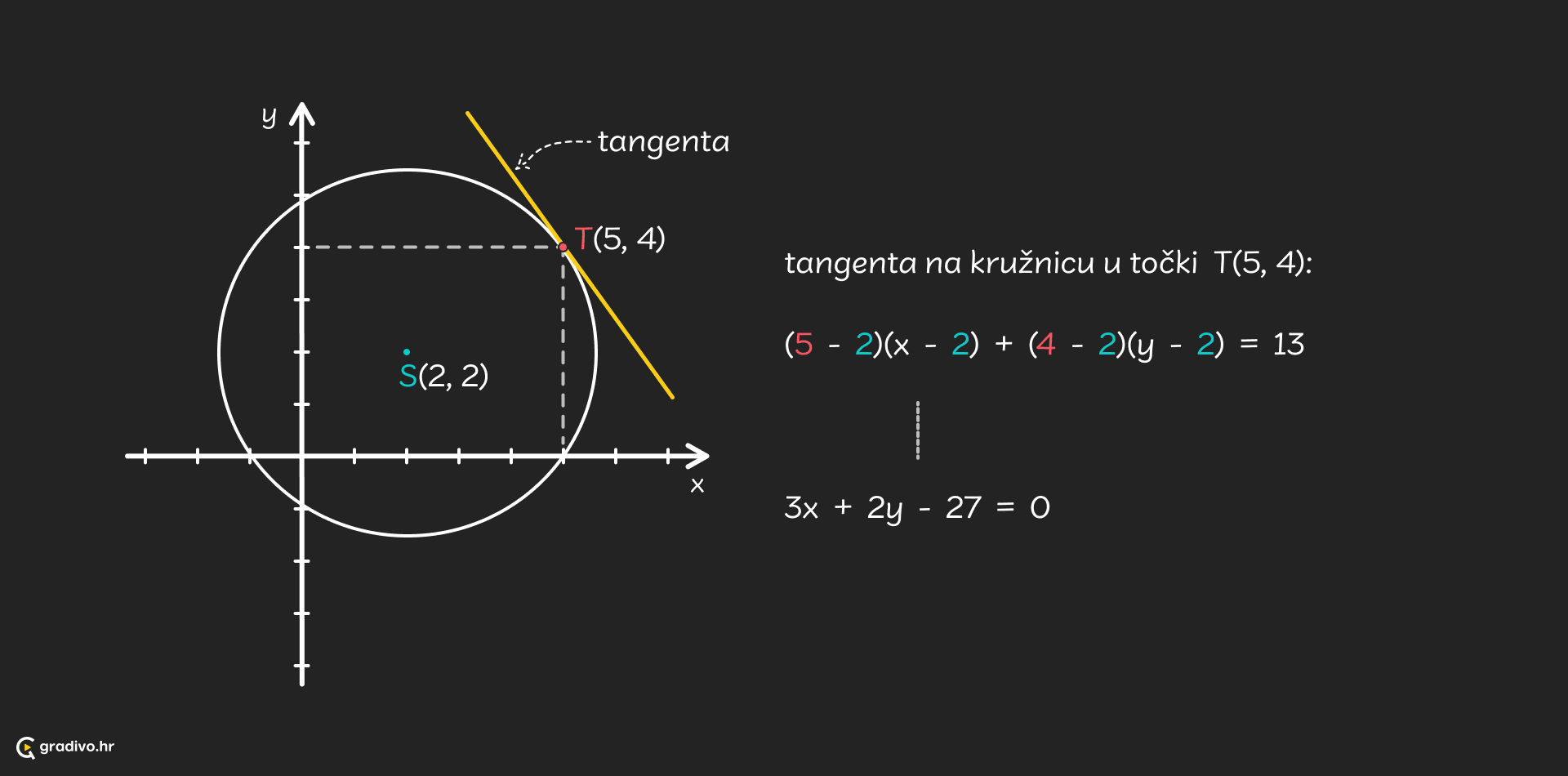
Napomena! Ako se traži tangenta na kružnicu iz točke $T(x_0,y_0)$ koja nije na kružnici, potrebno je riješiti sustav od dvije jednadžbe: jednadžba pravca koji prolazi točkom $T(x_0,y_0)$ i jednadžba kružnice.

Normala na kružnicu. Jednadžba normale u točki $T(x_0,y_0)$ na kružnicu je:

$ y-q=\frac{y_{0}-q}{x_{0}-p}(x-p) $
Normala na kružnicu u točki $T(x_0,y_0)$
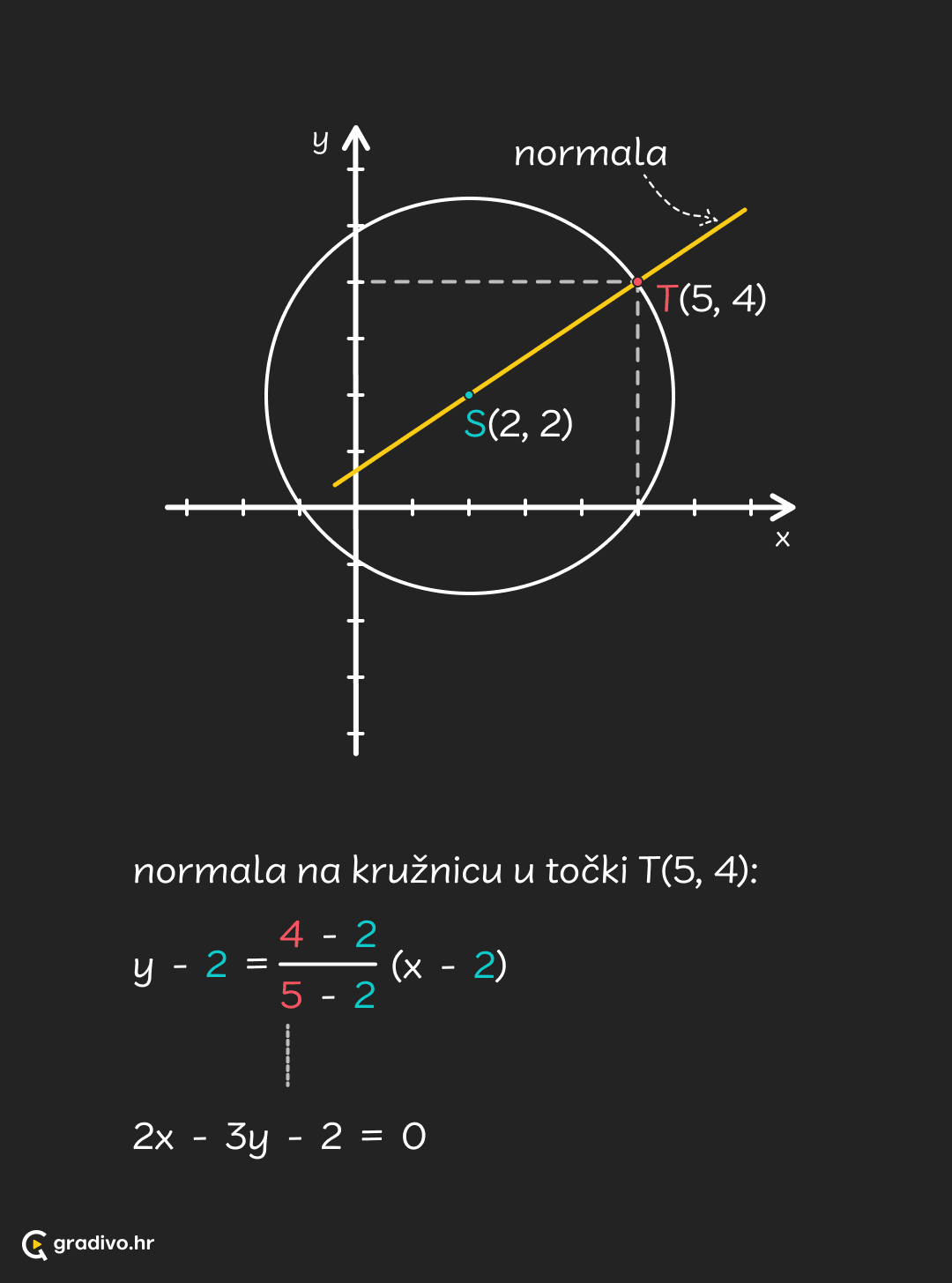
Tangenta_i_normala_-_mobile_1a6b3ca8d99c69e212f1d4a0e4643a823c2ccf1ff

Kut pod kojim pravac siječe kružnicu. Taj kut je kut između pravca i tangente na kružnicu u točki presjeka. Za koeficijent smjera pravca $k_1$ i koeficijent smjera tangente $k_2$ vrijedi da se kut $\alpha$ između pravca i kružnice računa kao:

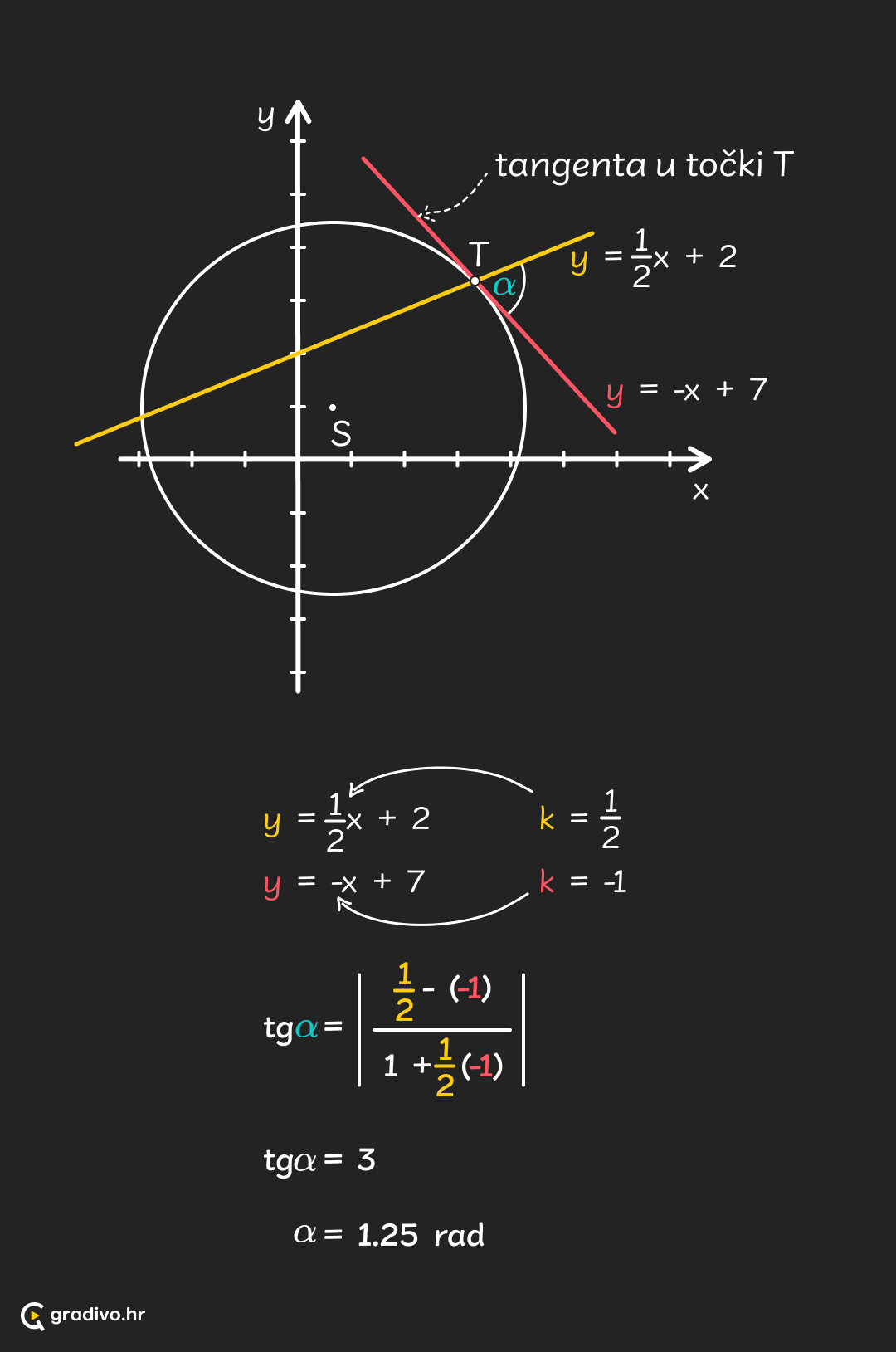
Tangenta i normala - mobile – 2
$ \operatorname{tg} \alpha=\left|\frac{k_{1}-k_{2}}{1+k_{1} k_{2}}\right| $
Kut pod kojim pravac siječe kružnicu

Međusobni položaj dviju kružnica

Dvije kružnice mogu se:

  • sjeći u dvije točke
  • imati jednu zajedničku točku (dirati se iznutra ili izvana)
  • uopće ne dodirivati.

Do sjecišta dviju kružnica (ako ih imamo) dolazimo rješavanjem sustava jednadžbi koji čine dvije jednadžbe dviju kružnica.

Kut pod kojim se kružnice sijeku. Kut između dvije tangente u točki presjeka tih dviju kružnica.

Cedevita Logo
ŠTO ČEKAŠ?

Isprobaj potpuno besplatno!

Registracijom dobivaš besplatan*
pristup dijelu lekcija za svaki predmet.

*Besplatan pristup ne zahtijeva unos kartice.
ZA MATURANTEOnline pripremeOD 1. DO 4. RAZREDAOnline instrukcije