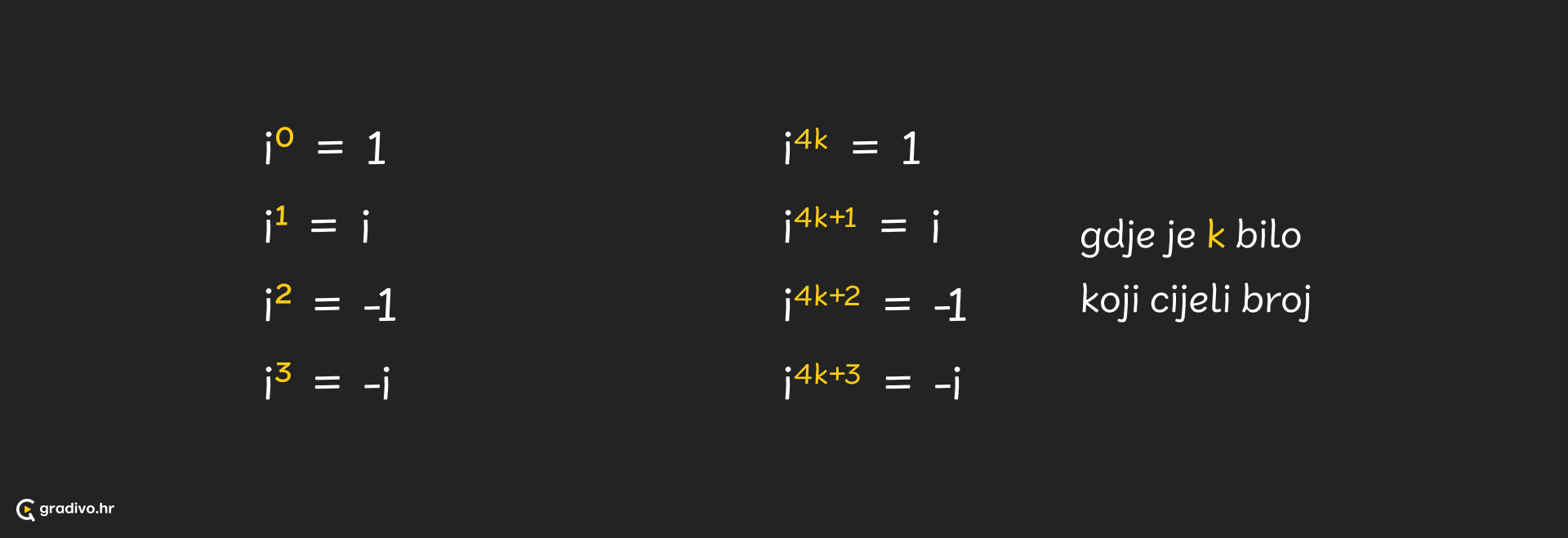Imaginarna jedinica, oznake $i$, je broj za koji vrijedi
Imaginarni broj je broj oblika $yi$ za neki realni broj $y$.
Kompleksni broj $z$ je broj oblika
U definiciji kompleksnog broja, $x$ i $y$ su obični, realni brojevi, a $i$ je i dalje imaginarna jedinica. Broj $x$ zovemo realni dio kompleksnog broja $z$, a $y$ je imaginarni dio.
Oprez! Imaginarna jedinica $i$ nije dio imaginarnog dijela kompleksnog broja $z$.
Oznake su:
$ x = \text{Re}z \quad \text{i} \quad y = \text{Im}z $
Dva kompleksna broja su jednaka ako su im jednaki i realni dijelovi i imaginarni dijelovi.
$ z=w \text{ ako je} \; \text{Re} z=\text{Re} w \; \text { i } \; \text{Im} z=\text{Im} w $
Potencije imaginarne jedinice
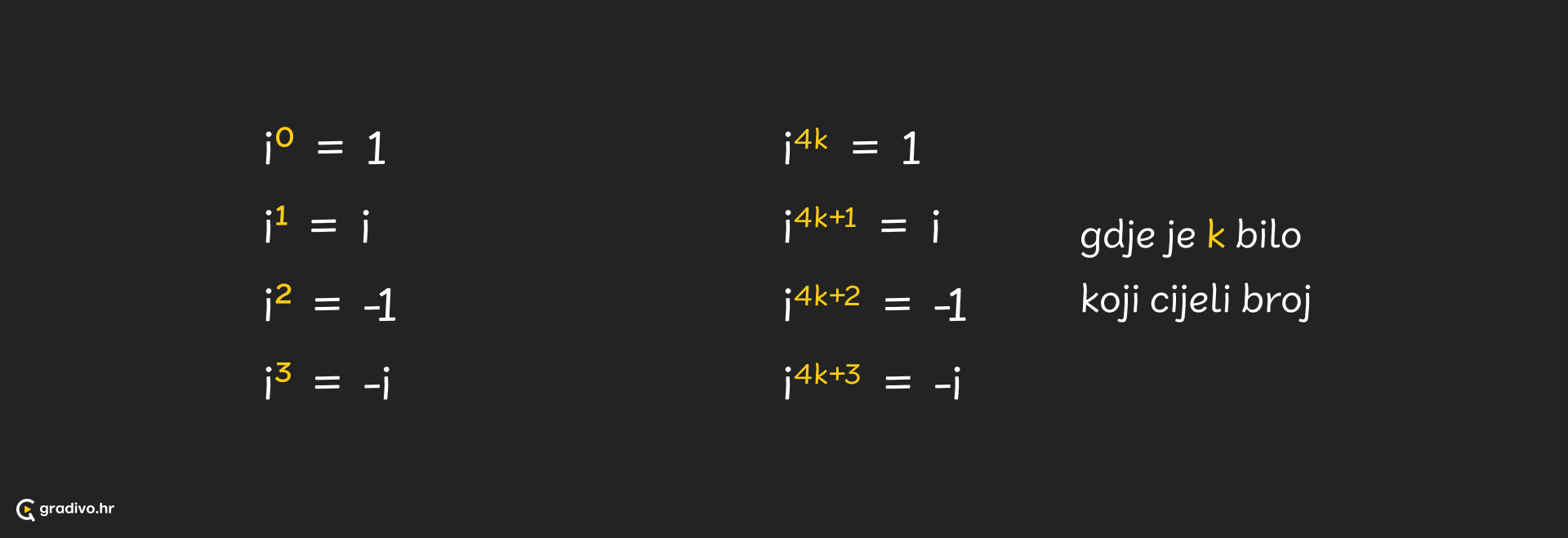
Računanje s kompleksnim brojevima
Uzmimo kompleksne brojeve $z=x_1+y_1 i$ i $w=x_2+y_2 i$ i pokažimo kako se oni zbrajaju, oduzimaju, množe i dijele.
$ z+w=x_{1}+x_{2}+\left(y_{1}+y_{2}\right) i $
$ z-w=x_{1}-x_{2}+\left(y_{1}-y_{2}\right) i $
$ z \cdot w=(x_1+y_1 i)(x_2 + y_2 i) = x_1 \cdot x_2-y_1 \cdot y_2+\left(x_1 y_2+x_2y_1\right) i $
Dijeljenje je malo drugačije. Zapišimo dijeljenje u obliku razlomka i slijedimo korake.
1. Da bi podijelili dva kompleksna broja, prvo se moramo riješiti imaginarne jedinice iz nazivnika. To radimo tako da zadani razlomak pomnožimo razlomkom koji i u brojniku i u nazivniku ima konjugirano kompleksni broj kompleksnog broja koji je kod nas u nazivniku.
2. Gore napravimo množenje kao što znamo, a dolje isto pomnožimo zagrade ili iskoristimo formulu za množenje kompleksno konjugiranih brojeva (nalazi se malo niže).
3. Sredimo što se da srediti.
Konjugirano kompleksni brojevi
Za kompleksni broj $z = x +yi$, kažemo da je $\overline{z}$ kompleksno konjugirani broj broja $z$ ako je $\overline{z} = x-yi$.
Umnožak kompleksno konjugiranih brojeva $z$ i $\overline{z}$ je:
$ z \cdot \overline{z} = (x+yi)(x-yi) = x^2+y^2 $
Modul kompleksnog broja
Modul kompleksnog broja $z = x+yi$, oznake $|z|$, je obični, realni broj koji računamo formulom:
$ |z|=\sqrt{x^{2}+y^{2}} $
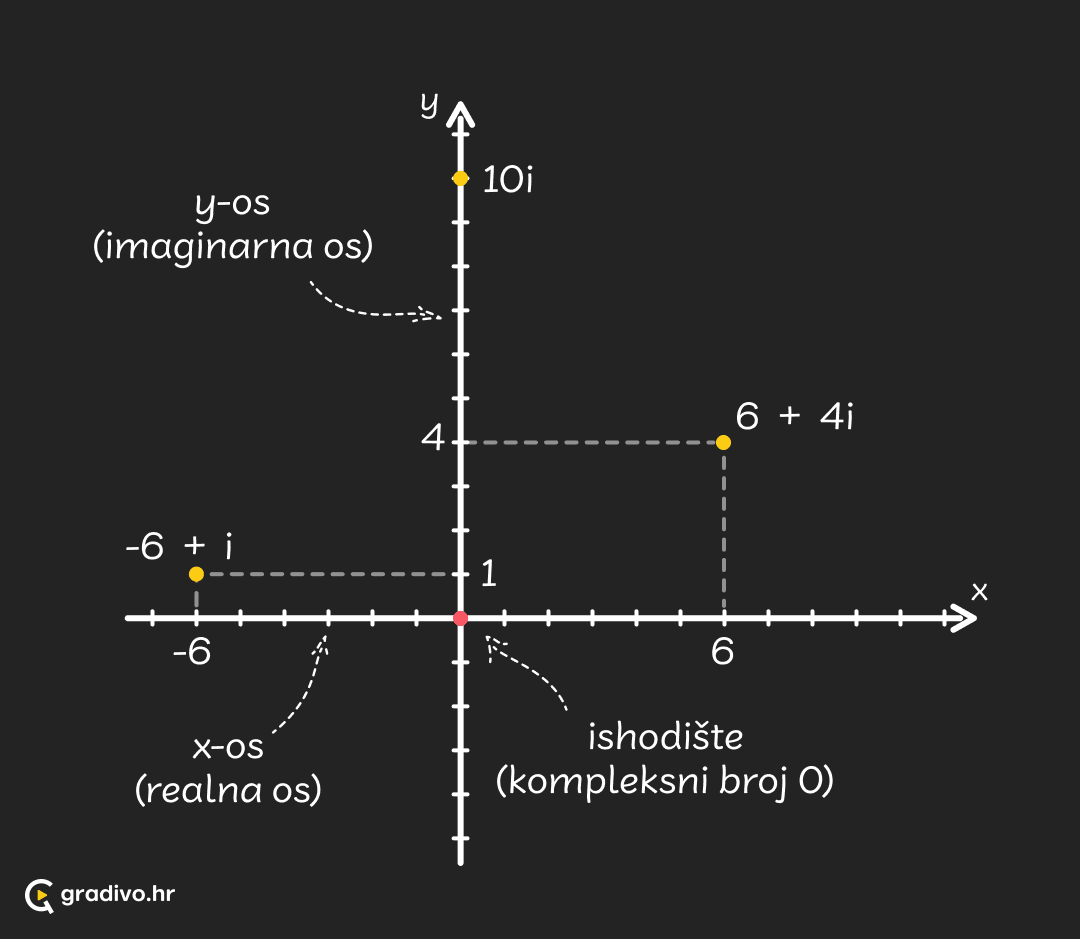
Kompleksna ravnina
Kompleksna (Gaussova) ravnina nam služi za prikazivanje kompleksnih brojeva u ravnini. Izgleda isto kao i obični koordinatni sustav, samo sada na $x$-osi označavamo realni dio kompleksnog broja pa je to realna os, a na $y$-osi imaginarni dio pa je to imaginarna os. Kompleksne brojeve (točke) ćemo označavati upravo po tom principu: broj $z=x+yi$ će odgovarati točki s koordinatama $(x,y)$.
Gore spomenuti modul će biti udaljenost točke od ishodišta. Ako želimo izračunati udaljenost dva kompleksna broja u ravnini, prvo ćemo ih oduzeti, a zatim izračunati modul dobivenog rezultata.
