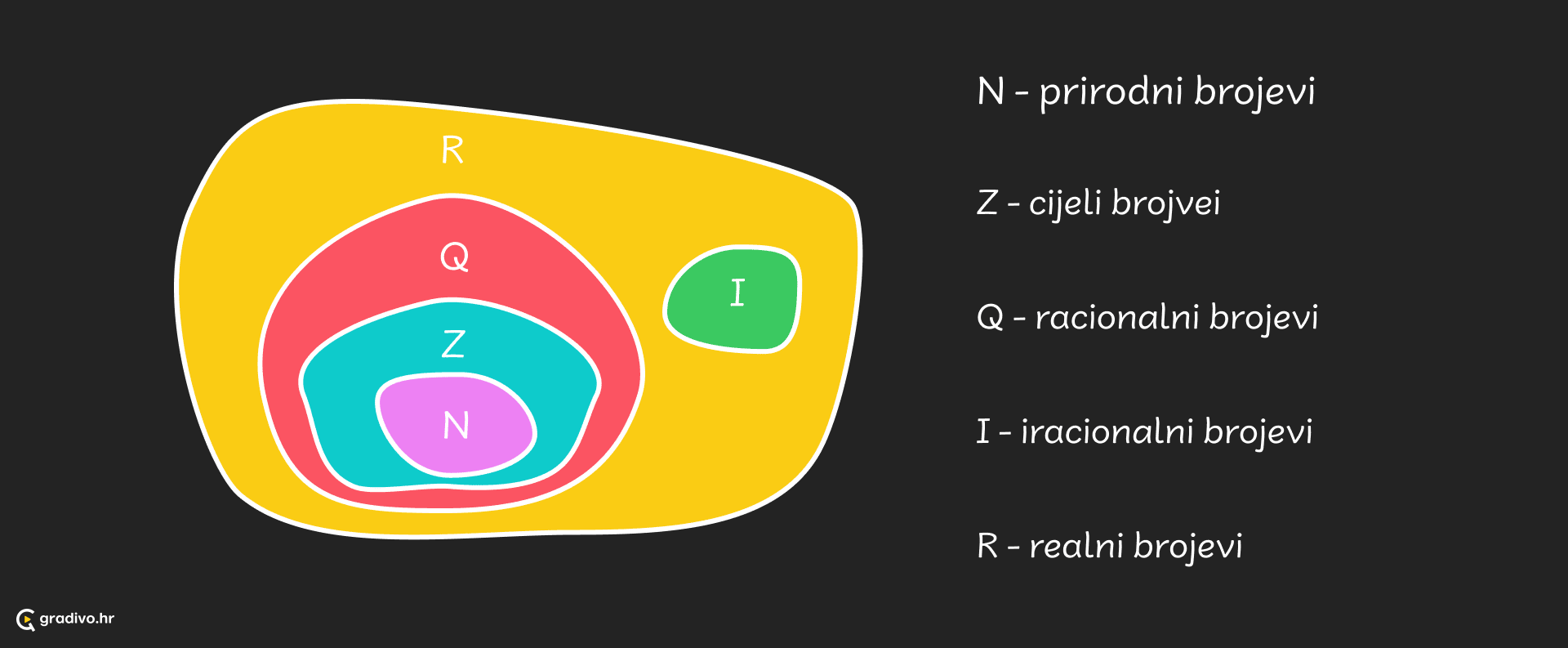
Skupovi brojeva

Računske operacije među skupovima
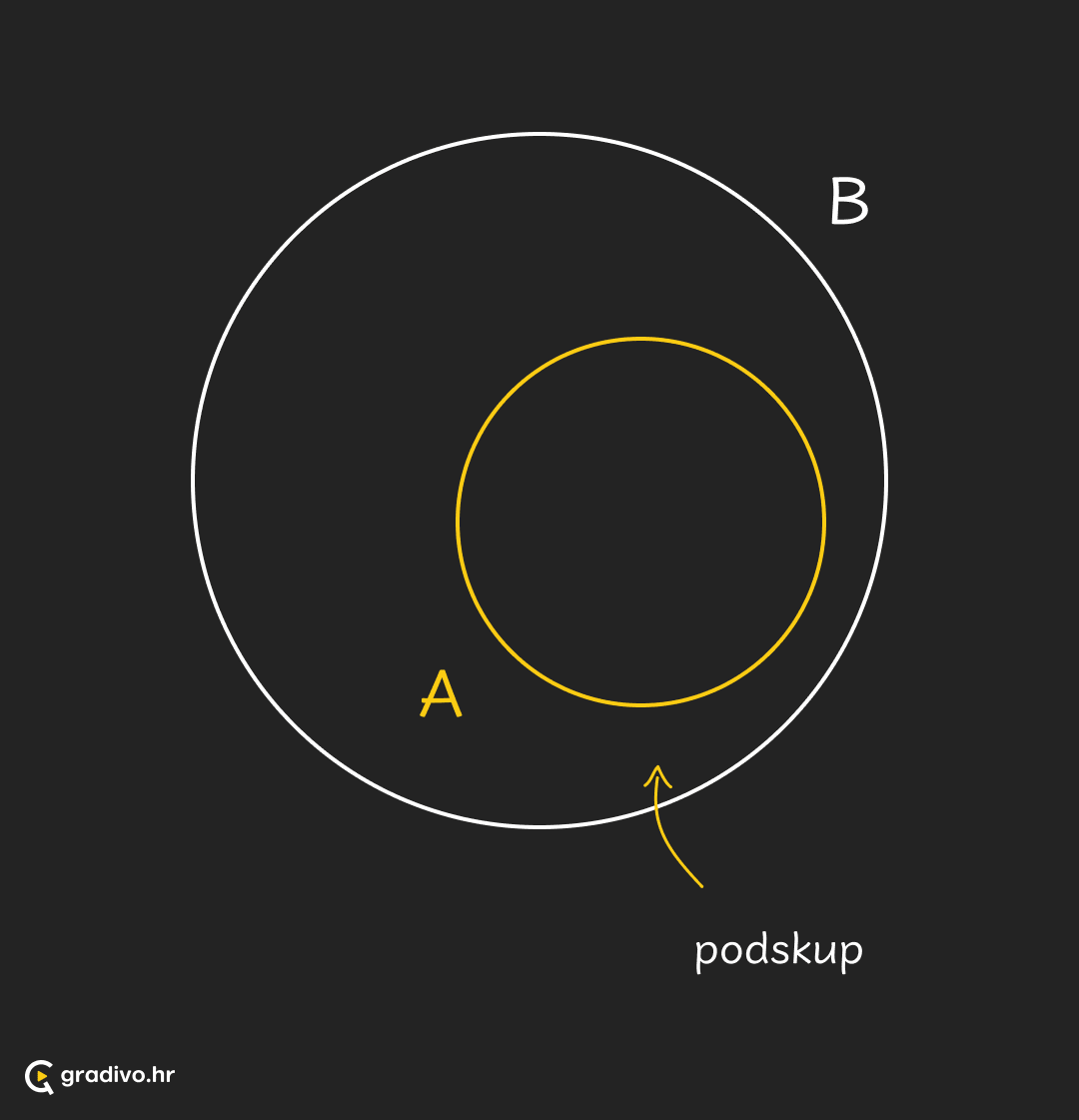
Kažemo da je skup $A$
Pišemo
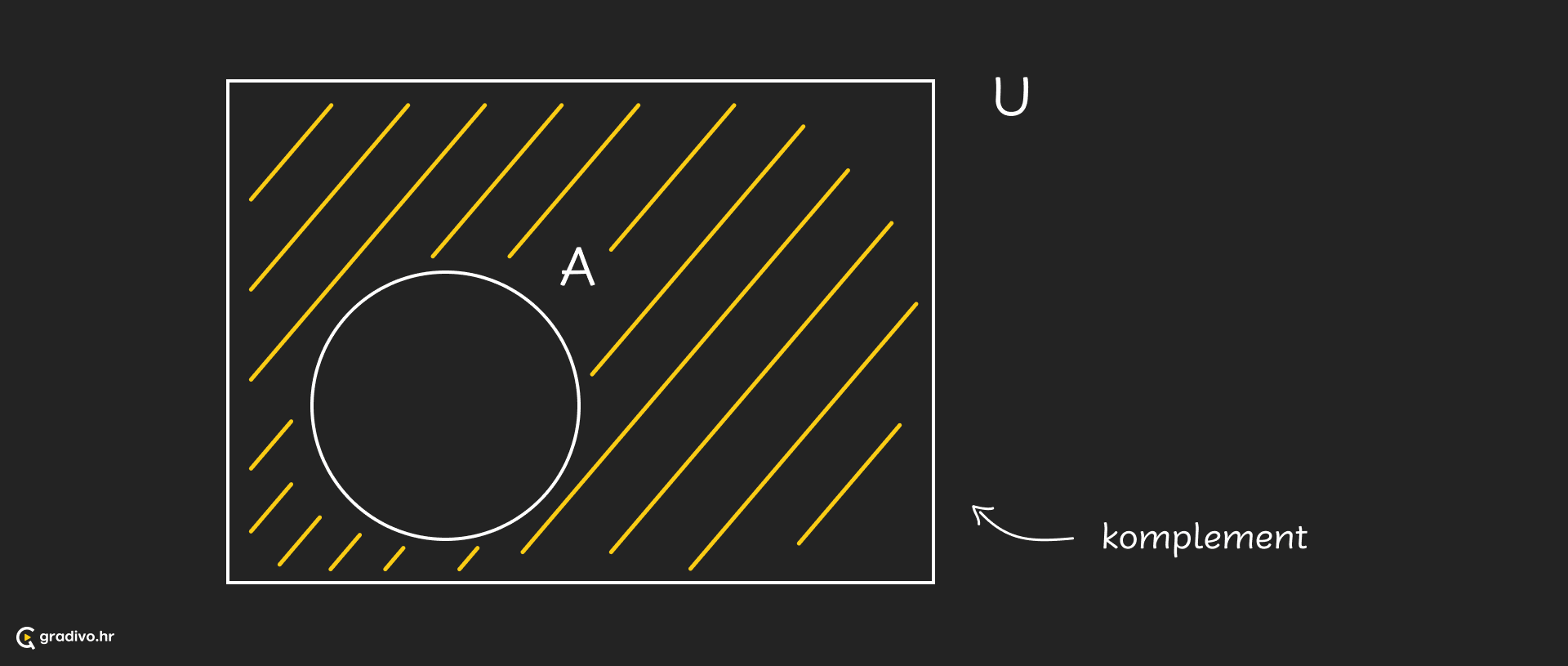
Ako unutar nekog skupa $U$ promatramo odnose među njegovim podskupovima, skup $U$ zovemo


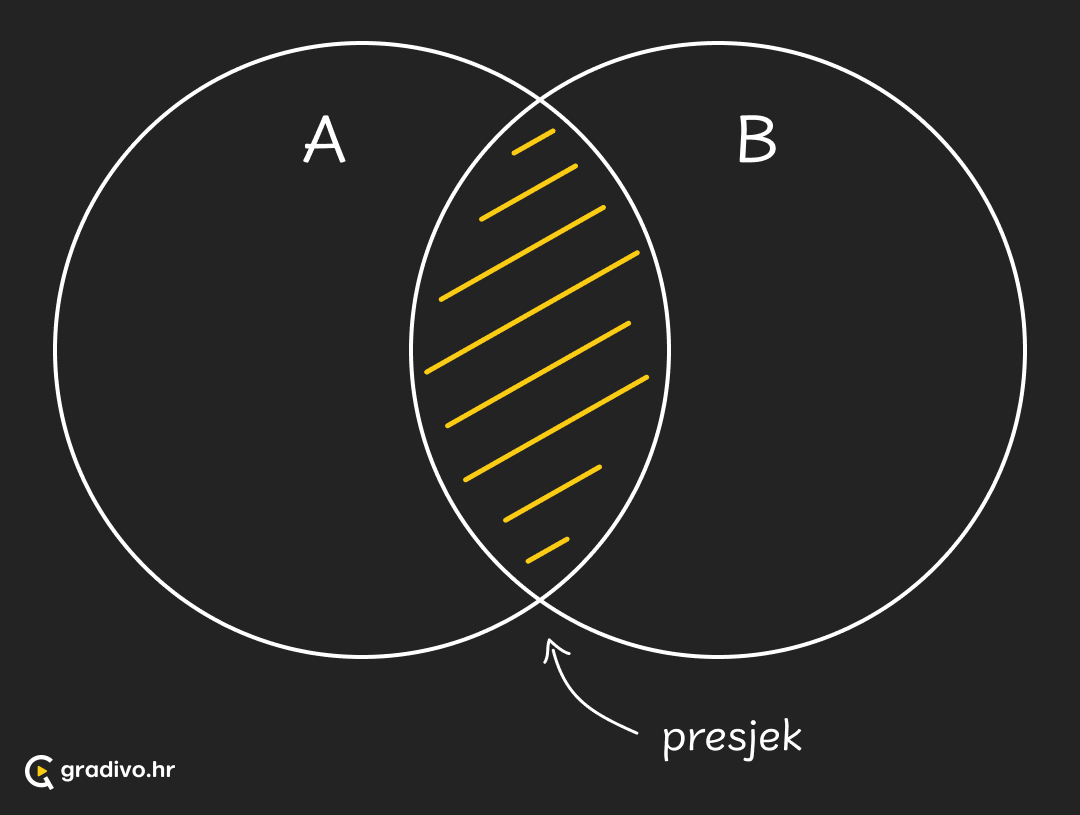
Ako skupovi $A$ i $B$ u presjeku nemaju zajedničkih elemenata, kažemo da su oni

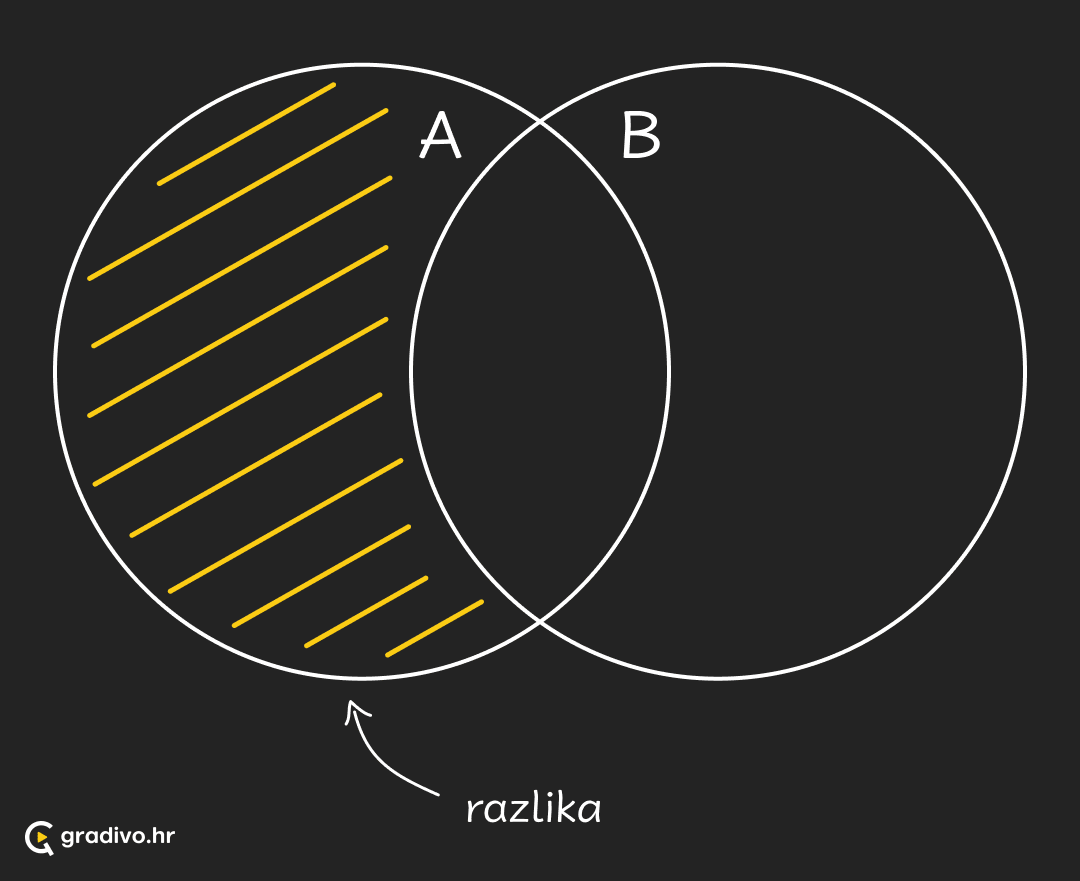
Neka je $A \subseteq U$.

Skup bez elemenata zovemo
Prisjetimo se sljedećih pojmova.
Prosti i složeni brojevi
Prirodne brojeve možemo podijeliti na proste i složene.
Broj $1$ nije niti prost niti složen broj.
Najveći zajednički djelitelj i najmanji zajednički višekratnik
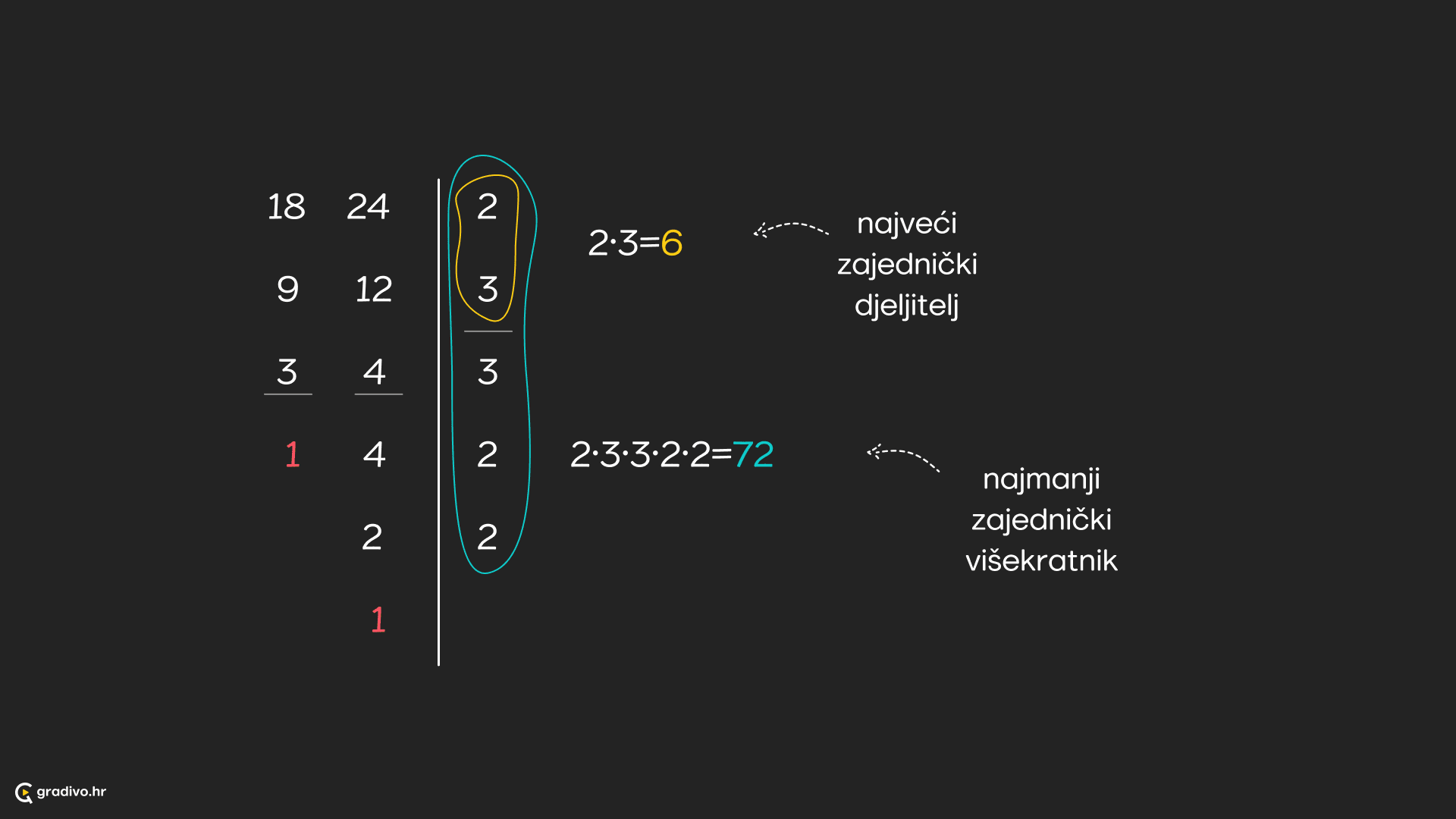
Najveći zajednički djelitelj dvaju brojeva dobijemo tako da istodobno oba broja dijelimo njihovim zajedničkim prostim djeliteljima dok je to moguće. U trenutku kada to više nije moguće, postupak je gotov. Umnožak tako dobivenih faktora je najveći zajednički djelitelj.
Najmanji zajednički višekratnik dvaju brojeva dobijemo tako da istodobno oba broja dijelimo njihovim zajedničkim prostim djeliteljima dok je to moguće. Zatim svaki od brojeva zasebno rastavljamo dalje na proste faktore dok ne dobijemo broj $1$. Umnožak svih tih faktora je najmanji zajednički višekratnik.
Najbolje ćemo objasniti na primjeru: nađimo $\text{nzd} (18, 24)$ i $\text{nzv} (18, 24)$.

Dijeljenje s ostatkom
U teoremu $q$ predstavlja najveći cijeli dio kvocijenta $b/a$, a $r$ ostatak pri dijeljenju.
Zapis racionalnih brojeva
Rekli smo da su racionalni brojevi su oni brojevi koje možemo zapisati u obliku razlomka npr. $\frac{m}{n}$ te se takav zapis zove razlomački zapis. Međutim, ako podijelimo broj $m$ brojem $n$ dobit ćemo decimalni zapis.
Prisjetimo se:
- $1.235$ konačni decimalni zapis
- $1.235235235235...=1.\dot{2}3\dot{5}$ periodički decimalni zapis
- $1.23535353535...=1.2\dot{3}\dot{5}$ mještovito periodički decimalni zapis
Također, možemo i obratno,
- decimalni broj koji ima konačan decimalni zapis pretvaramo u razlomak tako da u brojnik zapišemo taj broj bez decimalne točke, a u nazivnik pišemo broj $1$ i dodajemo onoliko nula koliko ima decimalnih mjesta
- ako broj ima periodički decimalni zapis, u brojnik zapišemo taj broj bez decimalne točke te oduzmemo onaj broj koji predstavljaju znamenke koje se ne ponavljaju, a u nazivnik pišemo broj $9$ onoliko puta koliko ima znamenki koje se ponavljaju
- ako broj ima mješovito periodički decimalni zapis, u brojnik zapišemo taj broj bez decimalne točke te oduzmemo onaj broj koji predstavljaju znamenke koje se ne ponavljaju, a u nazivnik pišemo broj $9$ onoliko puta koliko ima znamenki koje se ponavljaju, zatim broj $0$ onoliko puta koliko ima znamenki koje se ne ponavljaju, a nalaze se nakon decimalne točke
Najbolje ćemo uočiti na primjerima:

Isprobaj potpuno besplatno!
Registracijom dobivaš besplatan*
pristup dijelu lekcija za svaki predmet.