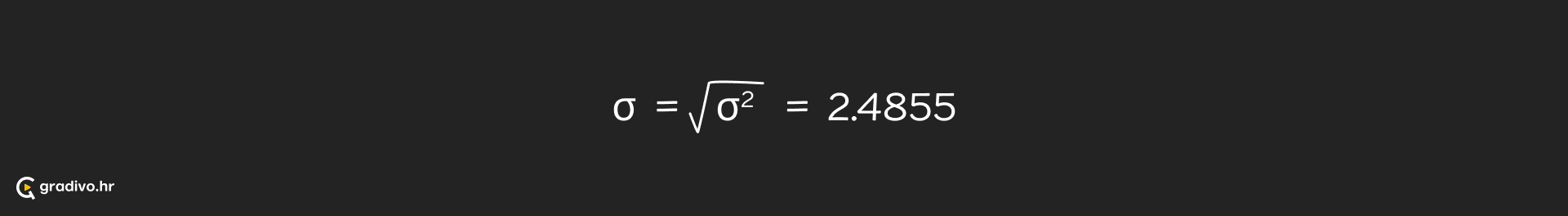Prikazivanje i analiziranje podataka
Skup iz kojeg uzimamo podatke zove se
Prikaz podataka
Podatke možemo prikazivati:
tablicom ( Prikazivanje podataka u obliku redaka i stupaca. Svaki redak predstavlja jedan podatak ili skup podataka, a svaki stupac kategoriju.)

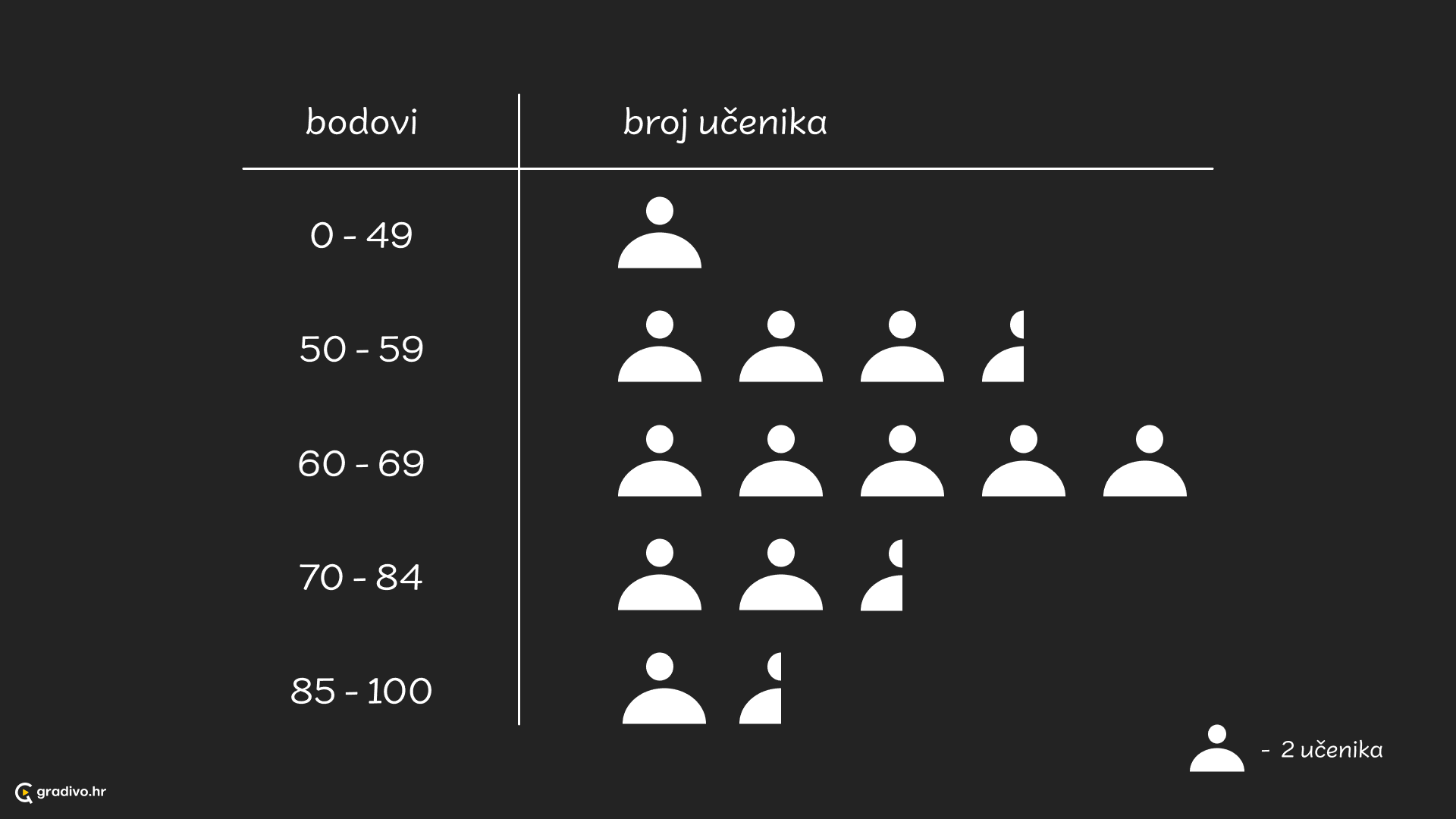
piktogramom (Prikaz podataka pomoću slika ili simbola, gdje svaki simbol predstavlja određenu količinu. Koristi se kad želimo prikazati podatke na vizualno jednostavan i razumljiv način.)

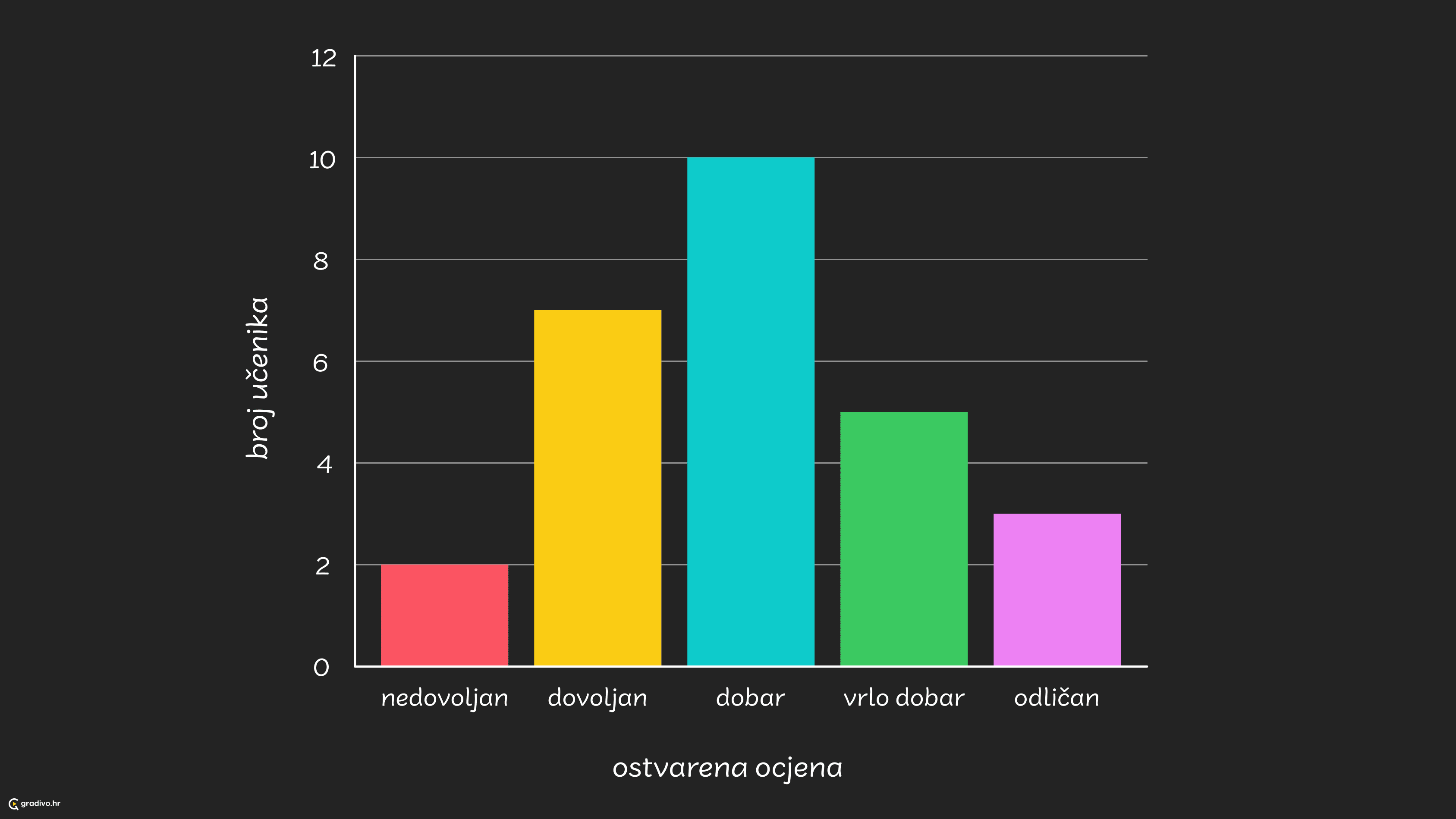
stupičastim dijagramom (Prikaz podataka pomoću vertikalnih ili horizontalnih stupaca. Svaki stupac predstavlja jednu kategoriju ili skupinu, a visina ili dužina stupca pokazuje veličinu podataka. Često se koristi za usporedbu različitih skupina podataka.)

dijagramom stablo - list (Grafički prikaz podataka koji se koristi za prikazivanje brojčanih podataka u formi stabla, gdje su listovi brojevi ili statistički podaci. Koristi se za organiziranje podataka u hijerarhiji i za prikazivanje odnosa među njima.)

kružnim dijagramom (Dijagram u obliku kruga koji je podijeljen na sektore, gdje svaki sektor predstavlja udio nekog dijela u odnosu na cijeli skup podataka. Koristi se za prikazivanje relativnih udjela.)

linijskim dijagramom (Dijagram koji koristi linije povezane točkama za prikazivanje promjena podataka kroz vrijeme. Najčešće se koristi za prikazivanje trendova ili kretanja podataka tijekom vremena.)

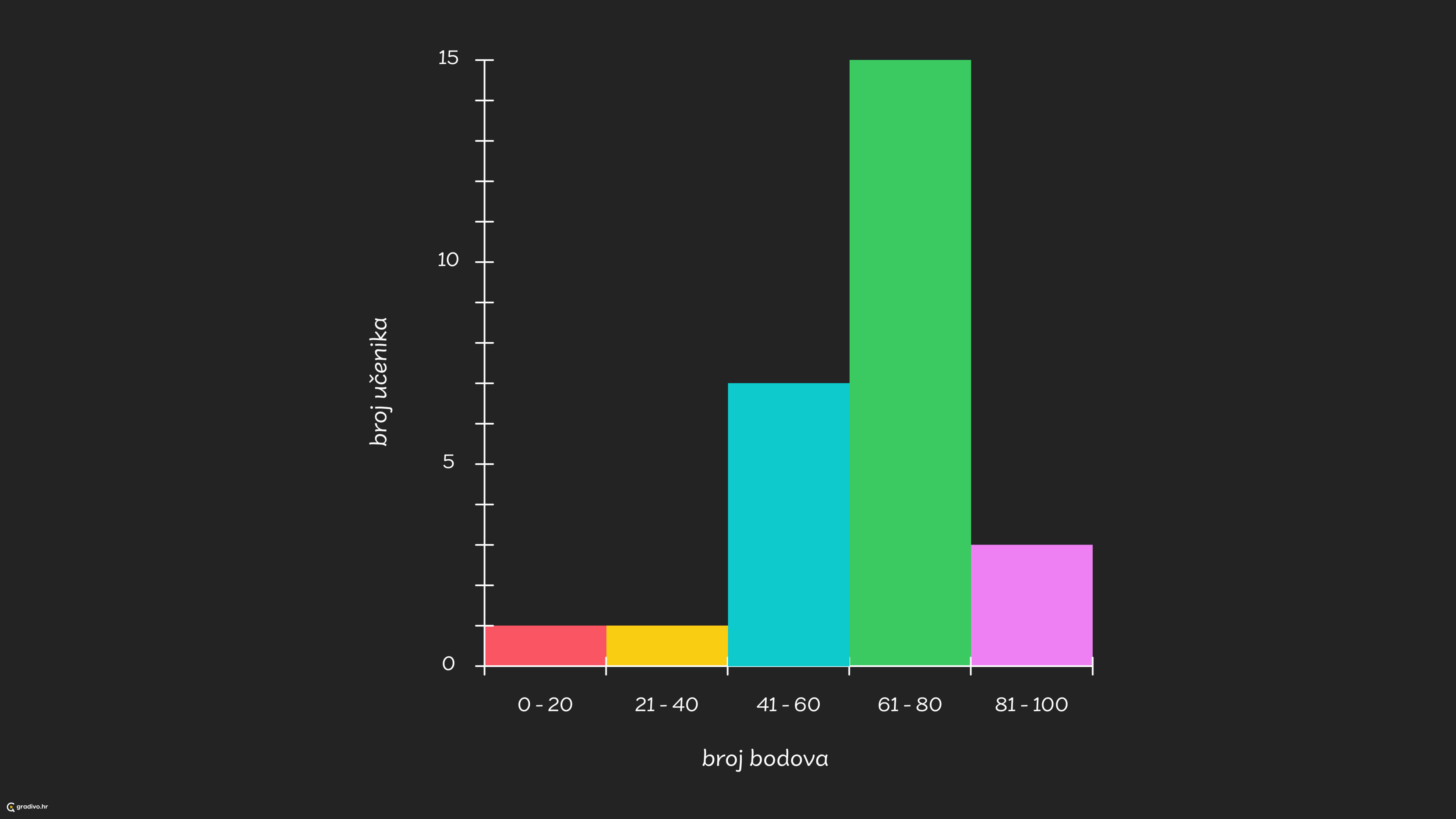
histogramom (Slično stupičastom dijagramu, ali koristi se za prikazivanje distribucije podataka unutar određenih intervala. Podaci se grupiraju u intervalima, a visina svakog stupca pokazuje koliko podataka spada u taj interval.)

Srednje vrijednosti
Neka su nam dani podatci: $x_1, x_2, x_3, ... , x_n$.
Da bismo lakše shvatili pojmove u ovom poglavlju, koristit ćemo sljedeći niz podataka:
Aritmetička sredina danog niza je:
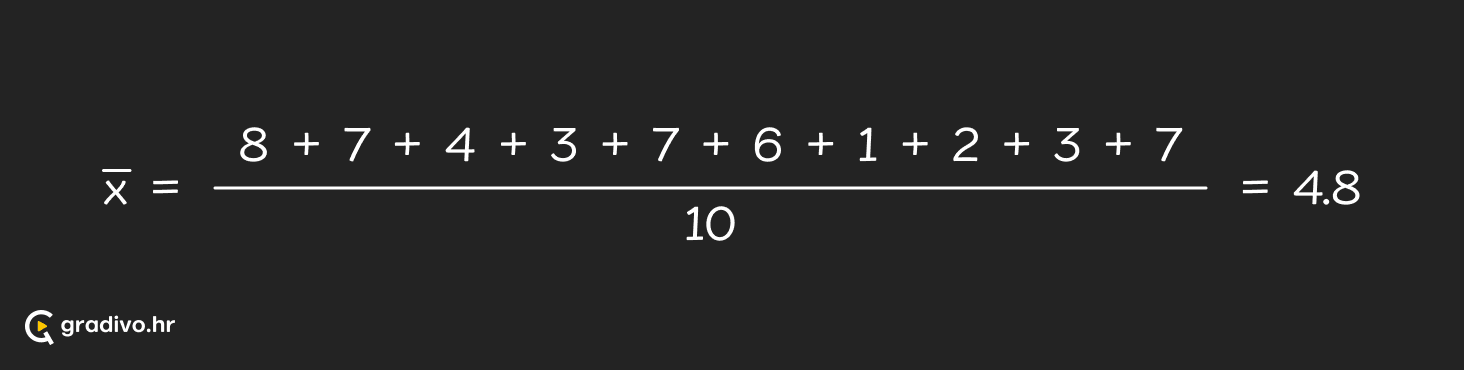
Mod danog niza je:
Za navedeni niz podataka vrijedi:

Rekli smo da medijan dijeli niz podataka na dva jednakobrojna niza. Na taj način dobivamo i kvartile:
prvi (donji) kvartil = medijan prve polovice niza odnosno "srednji" član tog dijela,$Q_1$ drugi (srednji) kvartil = medijan početnog niza,$Q_2$ treći (gornji) kvartil = medijan druge polovice niza podataka odnosno "srednji" član tog dijela,$Q_3$
Kvartili dijele niz podataka na četiri jednaka dijela.
Razlika između trećeg i prvog kvartila zove se interkvartilni raspon.
Brkata kutija
Ako želimo bolje prikazati skup podataka, možemo ih prikazati
- minimalna vrijednost svih podataka,
$X_{min}$ - prvi kvartil,
$Q_1$ - medijan (odnosno drugi kvartil),
$M_e$ ($Q_2$) - treći kvartil,
$Q_3$ - maksimalna vrijednost svih podataka,
$X_{max}$

Mjere raspršenosti
Neka su nam dani podatci: $x_1, x_2, x_3, ... , x_n$.
Neka je aritmetička sredina danih podataka $\overline{x}$. Broj
Za dani niz podataka varijancu i standardnu devijaciju računamo kao:

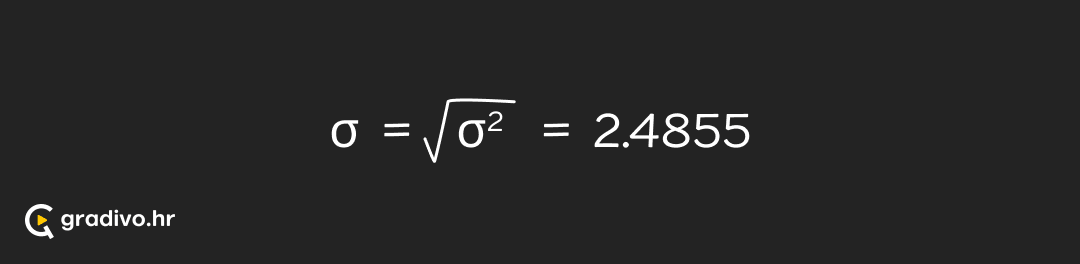
Isprobaj potpuno besplatno!
Registracijom dobivaš besplatan*
pristup dijelu lekcija za svaki predmet.