Matematika A - 2011. ljeto, 30.
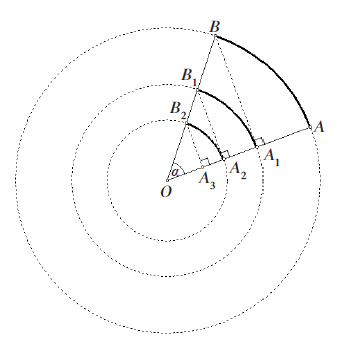
Na slici je prikazan niz koncentričnih kružnica sa središtem u točki $O$.a je mjera kuta $\angle A O B$ izražena u stupnjevima, a $|O A|=10 \mathrm{~cm}$.
Na polumjeru $O A$ leži niz točaka $A_{1}, A_{2}, A_{3}, \ldots$, a na polumjeru $O B$ niz točaka $B_{1}, B_{2}, B_{3}, \ldots$.
Točka $A_{1}$ je sjecište polumjera $\overline{O A}$ i okomice iz točke $B$ na taj polumjer.
Točka $A_{2}$ je sjecište polumjera $O A$ i okomice iz točke $B_{1}$ na taj polumjer itd.
Zbroj duljina svih kružnih lukova $\overparen{A B}+\overparen{A_{1} B_{1}}+\overparen{A_{2} B_{2}}+\ldots$ jednak je $\frac{5 \pi \alpha}{18} \mathrm{~cm}$.
Odredite $\alpha$.
Odredite $\alpha$.