Matematika A - 2018, jesen - 29.
29.1. Odredite opći član aritmetičkoga niza $\left(a_{n}\right)$ kojemu je peti član $\frac{51}{2}$, a šesnaesti 53.
$a_{n}=$
$a_{n}=$
29.2. Zadani su kompleksni brojevi $z=-\sqrt{3}+i, w=\frac{1}{8}\left(\cos \frac{5 \pi}{3}+i \sin \frac{5 \pi}{3}\right)$.
Izračunajte $z \cdot w$ i napišite rezultat u trigonometrijskome obliku.
$z \cdot w=$
Izračunajte $z \cdot w$ i napišite rezultat u trigonometrijskome obliku.
$z \cdot w=$
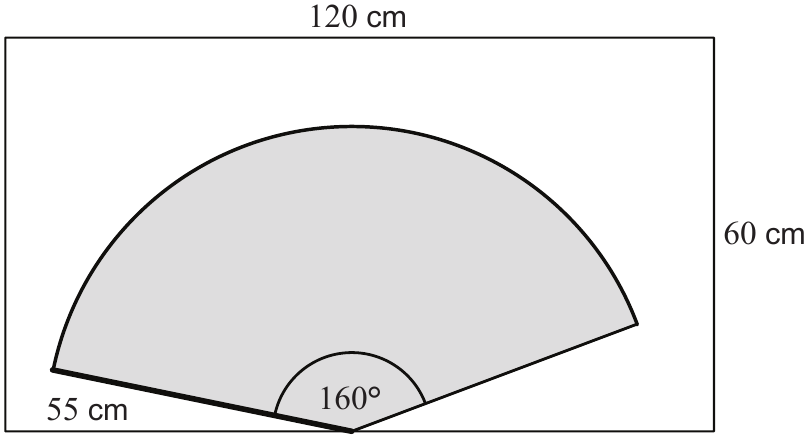
29.3. Brisač stakla dug je 55 cm i briše ravno staklo dimenzija $120 \mathrm{~cm} \times 60 \mathrm{~cm}$. Brisač se pri brisanju stakla zakrene za kut od $160^{\circ}$ kao što je prikazano na skici. Koliki postotak površine stakla brisač pritom obriše?
29.4. Visina pravilne uspravne četverostrane piramide je 9 cm , a duljina bočnoga brida 11 cm .
Izračunajte mjeru kuta između ravnine pobočke i ravnine osnovke te piramide.
Izračunajte mjeru kuta između ravnine pobočke i ravnine osnovke te piramide.
29.5. Umnožak prvih $n$ prirodnih brojeva je 272 puta veći od umnoška prvih $n-2$ prirodnih brojeva.
Odredite koeficijent uz $x^{15}$ u razvoju binoma $(x+4)^{n}$.
Odredite koeficijent uz $x^{15}$ u razvoju binoma $(x+4)^{n}$.